En un post anterior aprendimos qué es el mínimo común múltiplo y cómo calcularlo.
Hoy vamos a ver un par de ejemplos en los que utilizamos el mínimo común múltiplo (mcm) para resolver problemas matemáticos. Uno en el que directamente nos da la respuesta y otro en el que lo necesitamos como paso intermedio a la solución del enunciado.
mcm para resolver el problema directamente
El enunciado nos dice que en las dos islas hay la misma cantidad de monedas de oro, pero distribuidas de manera diferente. En una de las islas Bigotes de Lingotes encontrará las monedas de 8 en 8. En la otra el Pirata Barba Plata las encontrará de 36 en 36.
Ahora ya sabemos que si los piratas van sumando monedas de 8 en 8 por un lado, y de 36 en 36 por otro, los números en que coincidan ambas sumas pueden ser el número de monedas escondidas en cada una de las islas, porque en ambas hay el mismo número. O dicho de otra manera, el número de monedas en cada isla ha de ser a la vez múltiplo de 8 y de 36, y puede ser cualquier número que cumpla esta condición.
Pero nos piden el número mínimo de monedas que encontrarán. Es decir, de entre todos los múltiplos comunes de 8 y 36, el más pequeño. Hablamos del mcm de 8 y 36. 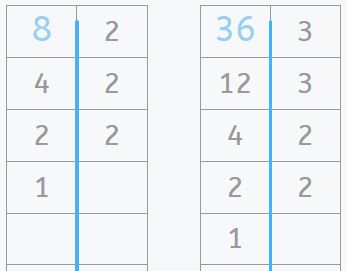
Así que Bigotes de Lingotes y el Pirata Barba Plata encontarán como mínimo 72 monedas de oro en cada isla.
mcm como paso intermedio para resolver el problema

Esta vez nos preguntan por el número de cajas de bates de béisbol que se han comprado como mímimo.
Para averiguar el número de cajas necesitamos primero calcular el número total de bates de béisbol que se han comprado como mínimo. Los bates de béisbol se han comprado de 15 en 15, y las gomas de 25 en 25. Además nos dicen que se han comprado la misma cantidad de bates de béisbol que de gomas. Así que el número mínimo de bates de béisbol que se han comprado es el mcm de 15 y 25.
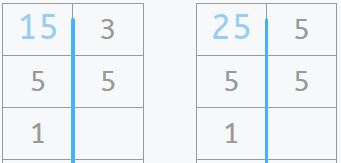

Ahora sabemos que como mínimo se han comprado 75 bates de béisbol, los mismos que gomas.
Sólamente queda dividir el número de bates entre los que hay en cada caja para averiguar cuántas cajas de bates de béisbol se han comprado como mínimo.

¡Eso es! Como mínimo se han comprado 5 cajas de bates de béisbol.
Si quieres seguir trabajando este tipo de ejercicios y otros muchos, entra en Smartick y pruébalo gratis.
Para seguir aprendiendo:
- Tabla 100 para calcular el mínimo común múltiplo (mcm)
- ¿Qué es el mínimo común múltiplo (mcm)?
- Problemas de operaciones combinadas
- Explicación de la fórmula para calcular el mínimo común múltiplo
- Divisiones con decimales usando el dinero como ejemplo
- Características de la práctica significativa - 23/03/2020
- Cómo representar fracciones en la recta numérica - 10/02/2020
- Diagramas de Venn en Smartick - 13/01/2020




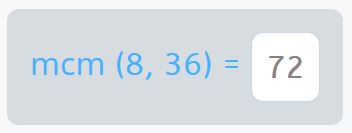





esta aplicación me sirvió bastante para mi aprendizaje matemático
Así es como debe ser la enseñanza de las matemáticas: con su aplicación en la vida diaria
*Muy. Buen problema y explicación 👍🏻*
¿Por qué en el MCM de 15 – 25 da 75?
¡Hola Jorge! El MCM de 15 y 25 es 75 porque es el número entero menor común múltiplo a los dos, es decir:
Los múltiplos de 15 son: 0, 15, 30, 45, 60, 75, 90…
Los múltiplos de 25 son: 0, 25, 50, 75, 100…
Por lo tanto, el mínimo común múltiplo de ambos números es el 75. ¡Espero haberte ayudado!
Gracias me ayudó mucho.
Hola quisiera aprender mas pero ustedes son lo maximo
me salvo para el examen de mi nueva escuela soy de 6to saludos de ecuador guayaquil