En este post seguimos analizando el libro de Craig Barton How I Wish I’d Taught Maths sobre la educación basada en evidencias. Hoy hablaremos del capítulo sobre el aprendizaje por analogías.
Aquí puedes revisar los posts anteriores que hemos escrito sobre el libro:
- Educación basada en evidencias. La historia de Craig Barton
- Relación entre pensamiento y aprendizaje
- Motivación. Educación basada en evidencias
¿Son las analogías buenas para el aprendizaje?
Una analogía bien planteada ayuda a los alumnos a conectar la nueva información con conceptos y habilidades que ya existen en su memoria.
Sin embargo, el aprendizaje por analogías no tiene un carácter mágico. Es necesario que haya un conocimiento que transferir. Es decir, que haya habido un trabajo suficiente en el dominio fuente (el modelo concreto).
Familiaridad y Visibilidad
Willingham (2009) identifica una condición necesaria para el éxito del aprendizaje por analogía: el modelo fuente debe ser familiar y los alumnos deben tener la oportunidad de experimentar con el modelo.
Si la analogía no es familiar o no se puede experimentar, los alumnos necesitarán utilizar gran parte de sus recursos cognitivos en entender el modelo. Además, cuando falte el material visual les resultará muy difícil producir la comparación relacional.
En cualquier caso, William (1997), concluye que la familiaridad y el poder experimentar con el modelo no son suficientes para saber si el aprendizaje por analogía es lo más adecuado para la enseñanza. Introduce otros dos criterios importantes.
Emparejamiento
El éxito de la transferencia en el aprendizaje por analogías depende de la semejanza estructural entre el dominio fuente y el dominio objetivo.
Sin embargo, el modelo fuente puede sufrir demasiados cambios al simplificarlo y por lo tanto dejar de asemejarse a su forma original. Esto puede provocar la obtención de inferencias erróneas.
Rango
¿Cuál es el rango de aplicación de la analogía? ¿Durante cuánto tiempo puede ayudar a nuestros alumnos para entender un determinado concepto?
Vamos a poner un ejemplo con los números enteros. Muchos maestros utilizan la analogía de las peras y las manzanas para explicar expresiones como 3a + 2b. No se puede sumar peras con manzanas. Sin embargo, esa analogía debemos abandonarla al encontramos expresiones de este tipo: 3a x 2b, pues es algo diferente que sí podemos combinar.
El termómetro es otra analogía que solemos utilizar para trabajar con los números enteros. Pero ¿realmente los niños saben hoy en día lo que es un termómetro cuando pueden mirar la temperatura en su smartphone?
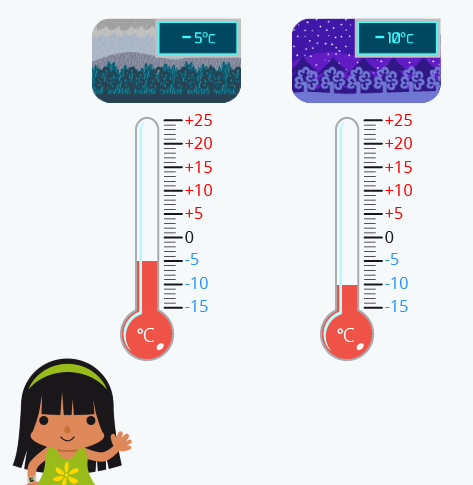
¿Podemos utilizar el termómetro para ayudar a entender todas las habilidades relacionadas con los números enteros?
- Para ordenar temperaturas negativas es perfecto: la temperatura de Burgos es -5ºC y la de Trevélez es de -10ºC. ¿Dónde hace más frío?
- Para sumar o restar números positivos sigue siendo también válido: ayer la temperatura de Burgos era de -2ºC, hoy ha bajado 5ºC más, ¿qué temperatura tenemos hoy en Burgos?
- Sin embargo, para sumar o restar números negativos deja de ser una analogía adecuada y empieza a resultar bastante forzada.
Una opción válida para representar este tipo de operaciones es el modelo de cargas. Sin embargo, es un modelo que no nos sirve para las multiplicaciones y divisiones de números enteros.
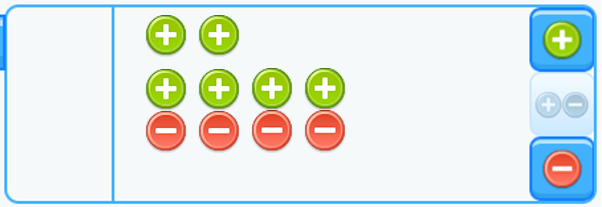
Llegados a este punto, no nos queda más remedio que abandonar también el modelo de cargas y utilizar el enfoque de la propiedad distributiva. La idea básica que hay detrás de esta justificación es utilizar el modelo de adición repetida para explicar el producto de negativo por positivo, cuando el negativo es el multiplicando.
![]()
Después deducir que el producto positivo por negativo es negativo empleando la propiedad distributiva.

En Smartick utilizamos las analogías de forma muy cautelosa, siguiendo algunas orientaciones del currículo y, por supuesto, tratando de no forzar la analogía más allá del límite.
Referencias:
- Willinghamm D. T. (2009) ‘Is it true that some people just can’t do math?’ American Educator 33 (4) pp. 14-19.
- William, D. (1997) ‘Relevance as MacGuffin in mathematics education’, British Educational Research Association Conference, York, September 1997.
Para seguir aprendiendo:
- Conociendo las escalas de temperatura: ¿Grados Celsius o Fahrenheit?
- Sumas y restas para niños: juegos, ejercicios y problemas para practicar
- Cálculo mental por asociación
- Rekenrek versus Sorobán I: La analogía con las manos
- Ubicar los diferentes números en la recta numérica
- Resolución de problemas de matemáticas - 24/02/2020
- Las cinco etapas de la práctica deliberada - 06/01/2020
- La auto explicación en el proceso de aprendizaje - 25/11/2019







