En el post de hoy vamos a estudiar el concepto de ratio desde la metodología de las «Barras de Singapur».
Primero debemos tener en cuenta que dos cantidades se pueden comparar de varias maneras diferentes: a través de una resta, a través de una fracción, a través de una multiplicación… pero en esta ocasión vamos a utilizar el ratio como factor de comparación.
Para poder comparar dos o más cantidades a través de un ratio deben de estar expresadas en la misma unidad. Una vez tengamos las cantidades unificadas debemos buscar la cantidad de una que hay con respecto a la otra.
Vamos a verlo a través de un ejemplo:
«Manuel y Javier son hermanos gemelos. Su madre les ha comprado una bolsa de bombones que contiene 4 bombones iguales. ¿Cuál es el ratio de bombones para los hermanos?»
El ratio de bombones con respecto a la cantidad de niños que hay, es de 2 bombones para cada niño y se expresa (2:1) y, como la relación es bidireccional, también se puede decir (1:2) que significa que hay un niño por cada 2 bombones
Ahora vamos a probar directamente con las barras de Singapur:
¿Cuál crees que es el ratio de 4 unidades naranjas para 8 unidades azules?
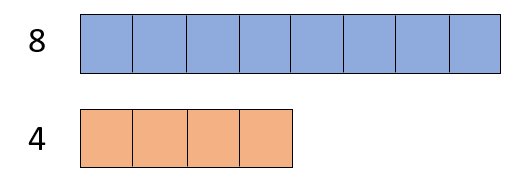
Pues la respuesta es la misma que en el caso anterior, 1:2 (hay 1 unidad naranja por cada 2 unidades azules) y 2:1 (hay 2 unidades azules por cada unidad naranja)
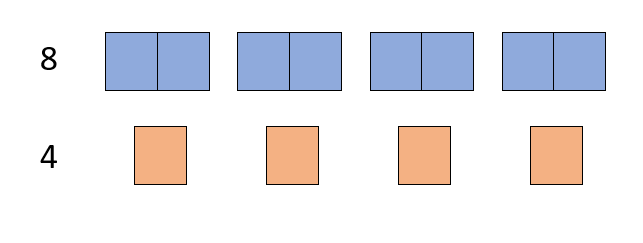
Ahora vamos a ver otro caso diferente, en el que las dos cantidades no son divisibles entre ellas:
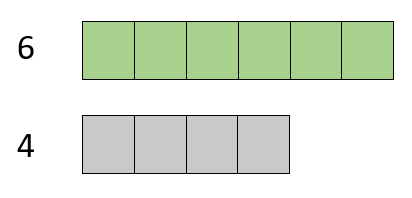
En este caso la relación es directa, el ratio entre estas dos cantidades no divisibles entre si es, 6:4 (6 unidades verdes por cada 4 unidades grises) y 4:6 (4 unidades grises por cada 6 unidades verdes)
Ahora vamos a comprobar que varias comparaciones de unidades pueden compartir el mismo ratio:
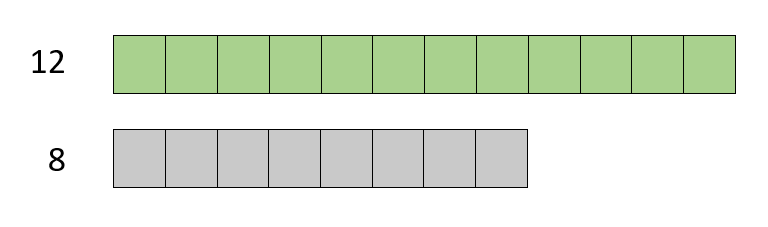
6 unidades verdes para 4 grises y 12 unidades verdes para 8 grises comparten ratio porque la relación que hay entre dichas cantidades es la misma.
Para saber más sobre este y otros temas entra, en Smartick y prueba nuestro método de aprendizaje de matemáticas de primaria.
Para seguir aprendiendo:
- Barras de Singapur aplicadas al concepto de porcentaje
- Barras de Singapur aplicadas a la multiplicación y división
- La decena y el sistema decimal
- Unidades, decenas y centenas
- Medidas de tiempo: bienio, lustro, década y siglo
Maestro de vocación y acción, forma parte del departamento de pedagogía de Smartick y trata de aportar la experiencia que ha ganado curso tras curso en el aula.
Cree ciegamente que no hay mejor forma de enseñar algo a un niño que a través de un manipulativo físico o digital.
“Aprender el qué a través del cómo”.
Me ayuda mucho
Muy bien entendí súper bien. Ya me quedó claro, muchas gracias espero que tengan muchas cosas más por explicar