El algoritmo tradicional de la división es de los que más trabas a la comprensión lógico-matemática plantea y, más aún, cuando los estudiantes empiezan a dividir por dos cifras.
Como el resto de operaciones matemáticas básicas (suma, resta y multiplicación), la división, también se puede expresar y comprender de diferentes formas: agrupamientos en un número concreto de grupos o en grupos de un número concreto de elementos. Ante estas dos definiciones, nuestra lógica actúa de formas diferentes, lo cual se puede ver cuando un niño resuelve un problema de reparto o agrupamiento sin haber oído hablar de la división pero, posteriormente, el algoritmo viene para sistematizar nuestro razonamiento lógico y “ponernos las cosas más fáciles”, unifica las definiciones de la división y lo resume en expresiones como: “0 al cociente y bajo la cifra siguiente”, “4 por 5, 25; al 28, tres y me llevo 2”, “tomo el 4, al 13 no cabe, así que tomo el 42” … que atentan contra nuestra lógica, pero resuelven divisiones.
Por eso en este post vamos a ver las dificultades que presenta el algoritmo tradicional de la división al aplicarlo a las divisiones por dos cifras y a explicar todo ese vocabulario que utilizamos, que parece referirse a una prueba de ensayo y error.
El algoritmo tradicional de la división presenta las mismas características, contradicciones y dificultades independientemente del número de cifras que tenga el divisor pero, cuando éste tiene solo una cifra, es más fácil mantener la idea del reparto o la agrupación que siempre conlleva la división; por ello nos centraremos en lo que ocurre al dividir por dos cifras. Así, podríamos decir que, este post explica el porqué de cada uno de los pasos que realizamos al dividir por dos cifras, como nos explicaba este post: Dividir por dos cifras
Paso 1: Seleccionar las primeras cifras del dividendo. Para ello hay que elegir tantas como tenga el divisor (en este caso dos, ya que vamos a dividir por dos cifras); este número ha de ser mayor que el divisor, si no, añadiremos una cifra más.

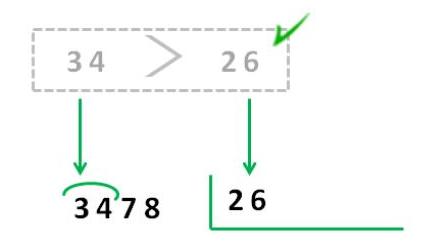
Aquí hay varios elementos que es importante comprender:
- La referencia la propiedad distributiva de la división: lo que estamos haciendo es, en este caso, dividir 3400 entre 26 para luego dividir los 78 que nos quedan entre los mismos 26 que indica el cociente
- El requisito de que esas dos cifras formen un número mayor que el divisor, es solo una cuestión de sencillez, porque, evidentemente, yo puedo dividir 3000 por 26.
Paso 2: Escribimos el primer número del cociente. Éste suele ser una cifra con el mismo valor posicional que el que tenían las unidades del “número de dos cifras” que ya habíamos elegido pero, la naturaleza del algoritmo nos impide expresarlo, es el número de grupos completos de 26 que yo puedo hacer con 3400 unidades; 100.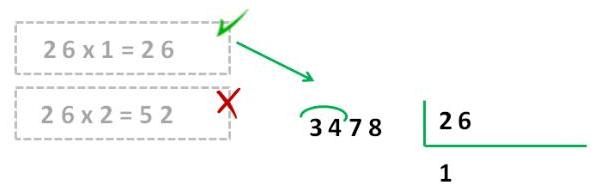
Paso 3: Dividimos las primeras cifras: “multiplicamos el cociente por el divisor y escribimos el resultado bajo el dividendo; después, hallamos la diferencia”. Aquí lo que estamos haciendo es calcular el resto, que es lo que no vamos a poder meter en nuestros grupos e 26, por eso, siempre ha de ser un número menor que el divisor, si no, significa que podríamos hacer otros, en este caso, 100 grupos más, porque estamos dividiendo centenas.
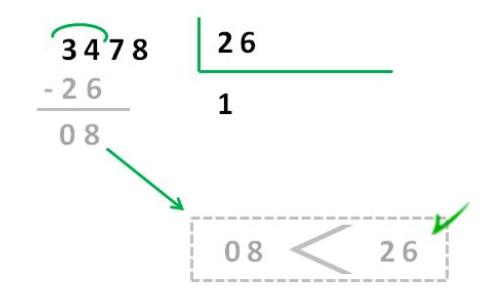
Paso 4: Bajamos la siguiente cifra y repetimos los pasos 2 y 3; por tanto debemos tener en cuenta las pautas anteriores:
- Propiedad distributiva de la división.
- Principio de sencillez.
- Valor posicional de los números.

Paso 5: Terminamos la división. Hasta llegar a dividir las unidades y, por tanto, no tener más que dividir, quedando el resto como indicador de aquello con lo que no hemos podido formar un grupo de 26 (siempre menor que el divisor).
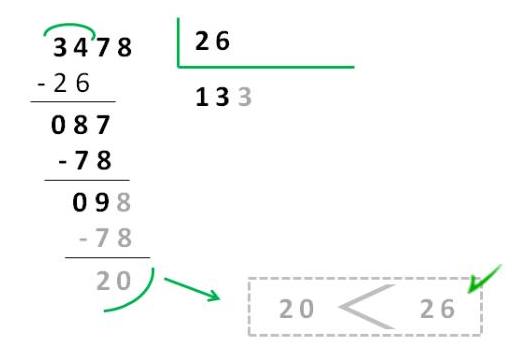 En Smartick nos parecen muy importantes tanto el proceso como el resultado, por ello, abogamos por la comprensión de la aritmética y no su memorización. Lo cual es complicado, sobre todo en los niveles de desarrollo cognitivo en que se empieza a trabajar con el alumno. Por ello, y para que sigas repasando, te propongo que veas este vídeo tutorial sobre las divisiones entre dos cifras.
En Smartick nos parecen muy importantes tanto el proceso como el resultado, por ello, abogamos por la comprensión de la aritmética y no su memorización. Lo cual es complicado, sobre todo en los niveles de desarrollo cognitivo en que se empieza a trabajar con el alumno. Por ello, y para que sigas repasando, te propongo que veas este vídeo tutorial sobre las divisiones entre dos cifras.
Y si quieres aprender más matemáticas de primaria, regístrate en Smartick y pruébalo gratis.
Para seguir aprendiendo:
- ¿Cómo se hacen divisiones de 3 cifras?
- Aprende a dividir por una cifra
- Cómo resolver una división de 3 cifras
- Divisiones de 3 cifras
- Divisiones de dos cifras: Ejercicios
- Number talks: Aprende matemáticas hablando - 31/05/2023
- Estrategias de cálculo mental para niños - 25/03/2021
- Ecuaciones reducibles: ¿qué son? ¿cómo se resuelven? - 03/02/2020








excelente material.
Muchas gracias 🙂
La mejor página de matemáticas, me salvó mi tarea. Saludos y que Dios te bendiga😘
Gracias.
la mejor página sobre matemática
¡Muchas gracias!