En este post vamos a explicar qué son las ecuaciones reducibles con varios ejemplos tomados de ejercicios que aparecen en las sesiones diarias de Smartick. Iremos de lo más sencillo a lo más complicado.
Si necesitas repasar antes qué es una ecuación y cuáles son sus términos, puedes hacerlo en este post anterior de nuestro blog.
Una ecuación reducible es una ecuación cuya resolución supone la «reducción» de su complejidad. Esto lo hacemos operando con sus términos hasta lograr una ecuación equivalente cuya resolución nos resulta más sencilla.
Ejemplo 1
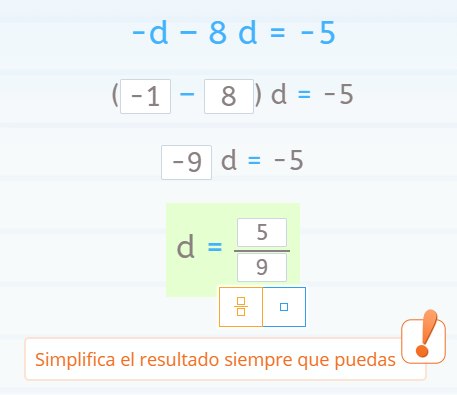
Nos encontramos con una ecuación reducible con incógnita (d) solo en uno de los miembros de la ecuación, pero descompuesta de forma aditiva (-d – 8d)
Es reducible porque tenemos que operar con estos monomios para después “eliminar” el coeficiente, “pasándolo” al otro miembro en forma de cociente.
Ejemplo 2
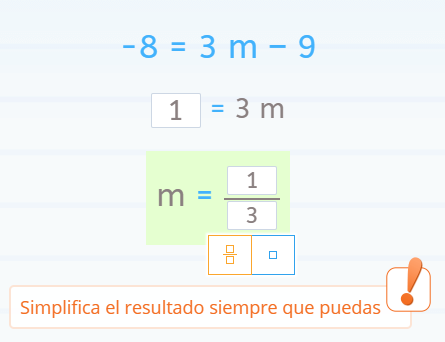
Estamos ante una ecuación reducible en la que la incógnita (m) está solo en uno de los lados de la igualdad, pero se relaciona de forma aditiva o multiplicativa con otro número.
Para aislar y despejar la incógnita, “pasaremos” estos números al otro miembro.
Ejemplo 3
En esta ecuación reducible por primera vez encontramos la incógnita (z) en ambos lados de la igualdad.
En este caso, lo primero que debemos hacer es unificar todos los términos con incógnita en uno de los miembros y dejar los demás en el otro miembro.
Es importante recordar que todos los términos se relacionan de forma aditiva, así que pasarán al otro término sumando o restando, nunca dividiendo o multiplicando. Esto solo ocurre cuando queremos pasar de un miembro a otro los coeficientes de las incógnitas. Lo cual tenemos que hacer en el último paso de este tipo de ecuaciones.
Ejemplo 4
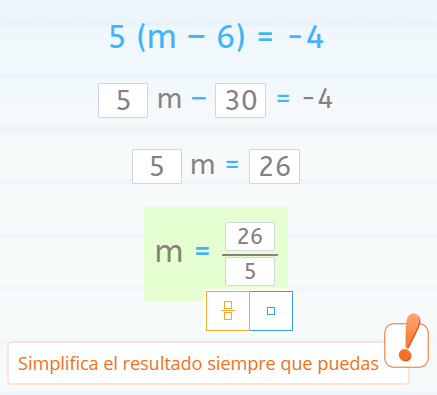
En este ejemplo encontramos una ecuación reducible que presenta un polinomio multiplicado por un factor común.
En este caso hay que resolver el producto y, luego, proceder como hemos hecho en el ejemplo anterior: cambiando de miembro el término independiente y, a continuación, eliminando el coeficiente de la incógnita.
Ejemplo 5
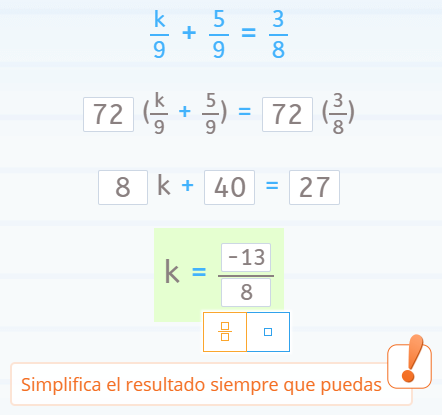
Este es el último ejemplo que vamos a ver. En este caso nos incomoda la existencia de denominadores en todos los términos de la ecuación.
Para reducir esta ecuación y encontrarnos con una ecuación más sencilla debemos hacer una ecuación equivalente. Para ello multiplicamos ambos miembros de la ecuación por el mismo número, el mínimo común múltiplo de los denominadores, para así poder simplificar todas estas fracciones.
Espero que con estos ejemplos hayas aprendido lo que son las ecuaciones reducibles y cómo operar con ellas. Si quieres seguir descubriendo las matemáticas, prueba Smartick gratis y no dejes de aprender 😉
Para seguir aprendiendo:
- Introducción a las ecuaciones
- ¿Cómo se resuelven los problemas de ecuaciones?
- Barras de Singapur aplicadas a la resolución de ecuaciones algebraicas I
- Las ecuaciones más importantes para la historia de la ciencia
- Fracciones con una incógnita
Forma parte del equipo de desarrollo de contenidos de Smartick, donde se encarga de elaborar secuencias didácticas, ejercicios y tutoriales. También colabora en la atención de sugerencias de los alumnos en "El Pozo".
Cree en la educación como motor de desarrollo de la sociedad y en el conocimiento como clave esencial para el crecimiento individual.
Sus pasiones son la educación en todas sus modalidades, montar en bici, el senderismo y escaparse de acampada siempre que puede.
- Number talks: Aprende matemáticas hablando - 31/05/2023
- Estrategias de cálculo mental para niños - 25/03/2021
- Ecuaciones reducibles: ¿qué son? ¿cómo se resuelven? - 03/02/2020