En el post de hoy vamos a aprender cómo resover ecuaciones algebraicas mediante el método de las “Barras de Singapur”.
Este método nos ayuda a visualizar gráficamente la información que nos dan en palabras en un problema de álgebra, lo que facilita muchísimo su resolución.
Veremos cómo resolver un ejemplo de problema algebraico con y sin modelización: En el campamento de verano de este año hay 50 niños y niñas. Si hay 10 niños más que niñas, ¿cuántas niñas hay?
Veamos cómo resolverlo primero por sin ayuda de la modelización y posteriormente con ayuda mediante el método de las barras de Singapur.
Resolución de ecuaciones sin modelización
Para resolver este problema directamente por el método algebraico de resolución de ecuaciones (sin modelización) podemos usar una letra, como x, para representar el número de niñas, que en principio es una cantidad desconocida:
x -> número de niñas en el campamento
Como hay 10 niños más que niñas, el número de niños es x + 10:
x + 10 -> número de niños en el campamento
El número total de niños y niñas será entonces x + (x + 10):
x + (x + 10) -> número total de niños y niñas en el campamento
Como nos dicen que el número de niños y niñas es 50, tenemos la siguiente ecuación para resolver el problema:
x + (x + 10) = 50
Quitando el paréntesis, tenemos:
x + x + 10 = 50
Asociando:
2x + 10 = 50
Restando 10 a ambos lados de la igualdad:
2x = 40
Y, por último, dividiendo entre 2 a ambos lados de la igualdad:
x = 20
Por tanto, obtenemos que hay 20 niñas en el campamento de este año.
Resolución de ecuaciones con modelización
En el método de las barras de Singapur podemos dibujar un modelo comparativo para representar la situación del problema, y usarlo para resolverlo mediante dos alternativas:
- Método unitario o el
- Método algebraico.
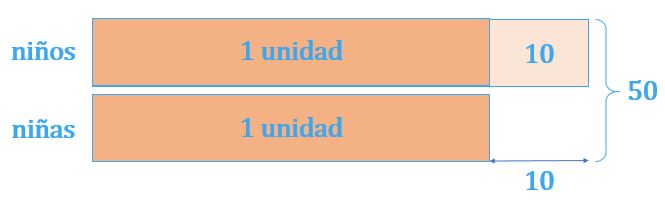
Este modelo muestra que el número total de niños y niñas es 50 y que la diferencia entre el número de niños y niñas es 10.
Con esta modelización, vamos a resolver ahora el problema primero por el método unitario y posteriormente por el método algebraico.
Primer método de resolución con modelización: Método unitario
Tomamos el número de niñas como 1 unidad. Podemos buscar el valor de 1 unidad y resolver el problema como sigue:
Como 2 unidades más 10 son 50:
Tenemos:
2 unidades + 10 = 50
Restando 10 a ambos lados de la igualdad:
2 unidades = 40
Y, finalmente, dividiendo entre 2 a ambos lados de la igualdad:
1 unidad = 40 : 2 = 20
Por tanto, como una unidad representa el número de niñas, obtenemos que hay 20 niñas en el campamento de este año.
Segundo método de resolución con modelización: Método algebraico
Como al principio, usamos la letra x para representar el número de niñas.
El modelo permite expresar el número de niños en términos de x como se muestra más adelante. Hay varias variaciones de este método, así que veremos una de ellas.
El número de niños es 10 más que el número de niñas. Esto es expresado como x + 10.
En el modelo se puede ver que x + (x + 10) es igual a 50, obteniendo la ecuación:
(x + 10) + x = 50
Procediendo como en los pasos anteriores, llegamos a que la solución a la ecuación es x = 20.
Nuevamente, como la letra x representa el número de niñas, obtenemos que hay 20 niñas en el campamento de este año.
¿Qué te ha parecido este método para modelizar un problema algebraico y facilitar su resolución? Espero que te haya parecido muy útil y lo puedas aplicar cuando resuelvas problemas de ecuaciones en clase y en tu vida cotidiana.
Si quieres seguir aprendiendo y practicando matemáticas de primaria, adaptadas a tu nivel, entra en Smartick y pruébalo gratis.
Para seguir aprendiendo:
- Barras de Singapur aplicadas a la resolución de problemas
- Ecuaciones reducibles: ¿qué son? ¿cómo se resuelven?
- ¿Cómo se resuelven los problemas de ecuaciones?
- Introducción a las ecuaciones
- Barras de Singapur aplicadas a la resolución de problemas II
Forma parte del equipo de desarrollo de contenidos de Smartick.
Amante de la naturaleza, el yoga y el baile.
- Valor absoluto de un número - 28/10/2019
- Cálculo de áreas de polígonos - 16/09/2019
- Potencias y su representación con regletas - 08/07/2019
excelente explicación
El método de las barras de Singapur está muy bien porque hace visual y gráfico la resolución del problema. Si de entrada lo resuelves algebraicamente se puede convertir en algo mecánico. Con este método te queda mucho mejor explicado, facilita la comprensión. Lo emplearé con los alumnos que tengo en mis clases particulares. Saludos