En este post vamos a aprender qué son las fracciones equivalentes.
Fíjate en la siguiente imagen:
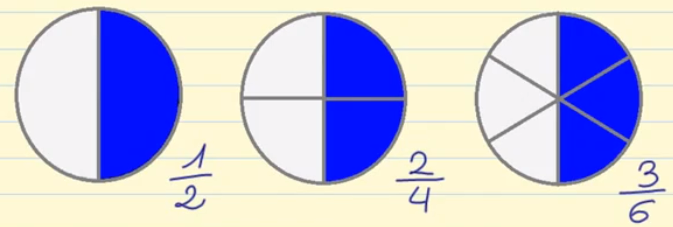
La primera figura está dividida en dos partes y hemos coloreado una de ellas. Por lo tanto, su fracción será 1/2.
La segunda figura la hemos dividido en 4 partes y hemos coloreado dos. Por lo tanto su fracción será 2/4.
Y la tercera figura la hemos dividido en 6 partes y hemos coloreado 3, por lo que su fracción será 3/6.
Si te fijas la parte coloreada en todas las figuras es la misma aunque las fracciones son diferentes: las tres fracciones dan el mismo resultado, son equivalentes.
Índice
¿Qué son las fracciones equivalentes?
Fracciones equivalentes son aquellas fracciones que representan la misma cantidad aunque el numerador y el denominador sean diferentes.
¿Cómo sabemos si dos fracciones son equivalentes?
Lo son si los productos del numerador de una y el denominador de la otra son iguales, es decir, productos cruzados.
Vamos a ver unos ejemplos:
Comprobemos si 2/5 y 4/10 son equivalentes.
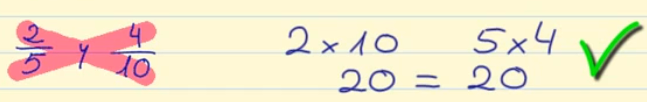
Para ello multiplicamos el numerados de una de las fracciones por el denominador de la otra.
2 x 10 = 20 5 x 4 = 20
Como el resultado es el mismo, podemos decir que 2/5 y 4/10 sí son fracciones equivalentes.
Ahora vamos a comprobar si 3/7 y 7/3 son fracciones equivalentes.
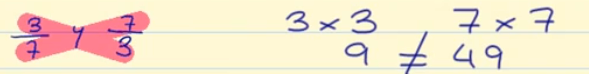
Para ello multiplicamos, como muestra la imagen:
3 x 3 = 9 7 x 7 = 49
Como el resultado no es el mismo, podemos decir que 3/7 y 7/3 no son equivalentes.
¿Cómo podemos calcular fracciones equivalentes?
Por amplificación
Multiplicando numerador y denominador por el mismo número.
Por ejemplo, partiendo de la fracción 1/3 y multiplicando el numerador y el denominador por el mismo número, podemos obtener diferentes fracciones equivalentes.
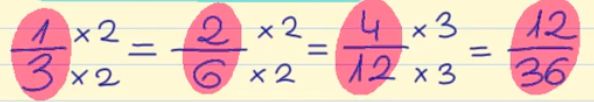
Si multiplicamos por 2: 1 x 2 = 2 3 x 2 = 6
por lo tanto la fracción 2/6 es equivalente a la fracción 1/3
Si volvemos a multiplicar por 2: 2 x 2 = 4 6 x 2 = 12
por lo tanto la fracción 4/12 es equivalente a 1/3 y a 2/6
Si ahora multiplicamos por 3: 4 x 3 = 12 12 x 3 = 36
por lo tanto 12/36 es una fracción equivalente a 1/3, a 2/6, y a 4/12
Vídeo tutorial sobre la amplificación
Echa un vistazo a este vídeo tutorial sobre la amplificación de fracciones.
Por simplificación
Dividiendo numerador y denominador por un divisor común de ambos.

Por ejemplo, 12/30 podemos dividir el numerador y el denominador entre 2, ya que tanto el numerador como el denominador son pares.
12 : 2 = 6 30 : 2 = 15
por lo tanto 6/15 es una fracción equivalente a 12/30
Ahora podemos dividirlos entre 3.
6 : 3 = 2 15 : 3 = 5
por tanto las fracciones 2/5, 6/15 y 12/30 son equivalentes.
Vídeo tutorial sobre la simplificación
Echa un vistazo a este vídeo tutorial sobre la simplificación de fracciones.
Si quieres practicar ejercicios con fracciones equivalentes, puedes hacerlo en este post anterior del blog de Smartick.
Y si quieres seguir aprendiendo muchas más matemáticas de primaria, adaptadas a tu nivel, regístrate en Smartick y pruébalo gratis
Para seguir aprendiendo:
- Cómo hacer una división de fracciones
- Convertir fracciones en números decimales
- Ejercicios con fracciones equivalentes
- Cómo resolver una suma de fracciones
- Pasar decimales a fracciones
- Tecnología en la educación escolar. Riesgos y beneficios - 31/08/2023
- Frustración y fracaso como instrumentos educativos - 13/04/2016
- Aquella sudadera del MIT y ahora Smartick - 17/11/2015








mi niña de 8 años necesita ayuda
Hola, Naneshka:
Muchas gracias por tu comentario.
Si quieres que tu hija aprenda matemáticas y refresque algunos conocimientos como las fracciones, basta con que te registres en Smartick. Tienes un periodo de prueba gratuito y sin ningún tipo de compromiso.
Si tienes alguna pregunta o duda adicional puedes escribir a mis compañeras del equipo pedagógico en [email protected]
¡Un saludo!
Buena información, me ayudó para el examen.
Excelente, muy sencilla de entender y comprender para poder explicar a mi nieta, aunque uno tiene ya el conocimiento a veces es difícil de transmitir de tal manera que ella entienda, pero con estos ejemplos se me hizo muy fácil de explicar y que comprendiera… Saludos y gracias.
Excelente blog…de mucha utilidad tanto para estudiantes como para los docentes…emplean un vocabulario sencillo y divertido que engancha de inmediato al lector
Muy buena explicación 🙂🙂🙂🙂 me ayudó con la tarea ♥️♥️♥️♥️😉👌
Me ha ayudado bastante a entender matemáticas.
Muy buena explicación, son muy buenos en explicar.
Me gusta mucho porque aprendo más rápido.
MUY BUENO
Es muy bueno 😃
me sirve mucho
muchas gracias 🫂👍😉👧🏻💟
me gustaría saber más la matemática con los signos que me cuesta entender tengo 65 años que estudio desde el año 1974 y quiero terminar la media
Hola Juan:
Muchas gracias por tu comentario.
Si quieres aprender más contenidos como estos y practicar matemáticas de primaria, basta con que te registres en Smartick. Tienes un periodo de prueba gratuito y sin ningún tipo de compromiso.
Si tienes alguna pregunta o duda adicional puedes escribir a mis compañeras del equipo pedagógico en [email protected]
¡Un saludo!
Muchas gracias por explicármelo tan bien, gracias a esta gran explicación he sacado un 10.
es muy buena
excelente material, muy didáctico y muy fácil de entender
me gustó mucho y aprendí bastante
excelente y muy didáctico. gracias
Excelente material, felicitaciones.
Muchas gracias por la explicación, me costaba mucho entender las fracciones equivalentes, soy docente.
muy completa la informacion
Excelente! Claro y preciso. Gracias x la ayuda. Soy docente.
lo amé, es genial me ayudó a estudiar para mi examen de mate
Sí me gustó la explicación, es en donde no entendía.
Gracias por simplificar mi trabajo con mis alumnos. Muy buen trabajo el que realizan.
Me lo sé mejor mil gracias 10/10
Me ha encantado mucho la forma de explicar.
Mil gracias
muy bien explicado paso a paso
Genial 😁
Ya me lo sé muchísimo mejor 👍🏻
10/10
Excelente apoyo muy claro y fácil de entender. Gracias
muchas gracias
Muy buenos días. Muy buena la temática, se entiende muy bien.
Gracias por éste medio de aprender.
EXCELENTE AYUDA EDUCATIVA, TERMINOS Y TUTORIALES FACILES DE ENTENDER. AGRADECIDOS.
Sirve mucho para los niños
Excelente artículo. Muy didáctico. Agradecida.
Es muy buen material para ayudar a nuestros hijos. Me parece bien que nos ayuden a realizar las actividades de nuestros hijos..
gracias enserio esta página ayuda mucho
Excelente!!! Me ha sido de gran ayuda. Muchas gracias.
Muy bueno para apoyar a mis hijas
Quiero saber cual es el equivalente de la fracción 2/4 que tenga 6 como numerador
Si has multiplicado por 3 el numerador (2×3=6) debes hacer lo mismo con el denominador…
Muy bien explicado gracias a esta página mi hija sacó un 20 en matemáticas la recomiendo muy buena
muy bien explicado gracias
Es muy buena la aplicación para aprender matemáticas. Muy importante para mí, gracias.
Muchas gracias, me ha ayudado mucho su explicación. Espero continuar obteniendo información tan detallada y útil. De nuevo, mil gracias.
es muy bueno, me sirve de mucho
Super gracias
Es muy importante para aprender cada día más y más. Gracias.
Genial, gracias por compartir
Muy buena
¡¡Muy bien!!
¡Me gustó mucho!
¡Bien!
¡bien!
Es muy buena, me gustaron las explicaciones, claras y sencillas
Gracias
Gracias, me ayudaron para mi examen
Excelente explicación, muy objetivos y buena metodología.
¡Excelente!
MUY BUENA EXPLICACIÓN Y MUY DIDÁCTICA, ME GUSTARÍA SEGUIR RECIBIENDO MÁS TEMAS, PARA BÁSICA SUPERIOR. UN SALUDO DESDE ECUADOR.
Excelente material, muchas gracias.
excelente !!!!me sirvió mucho, fue de gran ayuda gracias.
Me sirvió mucho gracias ☺😁🤩
Me encantó toda la explicación. Está tan bien explicado todo, uno por uno, que bueno. Saludos desde Venezuela
Está muy bueno
Gracias, muy útil para aprender, me sirvió mucho.
gracias 😀
gracias
Buenos días… Desde todo punto de vista ese material me ha parecido excelente! Felicitaciones y gracias!
Es el mejor.
Me gustó mucho el vídeo y la clase gracias.
Increíble explicación, muchas gracias 🙂
Excelente, muy buena la explicación.
Muy buen trabajo 😄
Gracias
muchas gracias me sirvio de mucho porque tenia una tarea de matematicas de fracciones equivalentes…. y soy del curso: 801
muchas gracias
Buenas explicaciones 😉
Entendí bien la explicación
Buenos días: para encontrar las fracciones equivalentes multiplico numerador y denominador por un mismo número. ¿Ese número puede ser una fracción? Obvio de manera tal que me queda otra fracción equivalente con números enteros…( por definición de fracción)
Me ayudó a entender mejor
me gustaron mucho y aprendí, gracias
Entendí muy bien
muy bien explicado
me ayudó mucho
GRACIAS
Esto es fabuloso y encantador
Me ayudó mucho
muy bueno me ayudó a entender mas
Me ayudó a entenderlo y me gusto
Excelente, me ayudó mucho con mis dudas.
me sirvió gracias
Muy clara la explicación, aprendí gracias…
Gracias. Excelente trabajo.
EXCELENTE EXPLICACIÓN, GRACIAS.
Gracias
Excelente se aprende muy bien
Gracias
Entendí con los ejemplos
Excelente información. Me ayudó mucho. Gracias.
esto me sirvió en aprender mas sobre fracciones y aprendí como saber si son equivalentes
magnífico
Hola muy buena explicación me sirvió para hacer un trabajo de las fracciones GRACIAS!!!
Gracias súper bueno
Gracias!
Fue muy útil y de fácil comprensión
gracias muy bueno
muchas gracias me sirvió de mucho
Es un excelente material muchas gracias.
Me ayudaron mucho por eso les doy un beso grande,💝👄😘😍🤩❤️❤️💝🌺😍🤩❤️💝🌺😍🤩❤️💝 love 🤩❤️❤️💝👄😘
Muy buena y fácil de entender la explicación
bueno me ayudó mucho gracias
Muy buenos ejemplos
Excelente me ayudó mucho, gracias
gracias. me ayudó mucho, es genial
Es buena la página
Gracias por la información es super comprensible y muy fácil de aprender
Muchas Gracias¡¡¡¡¡¡
me parece interesante para enseñar con ejemplos a los alumnos, asi difícilmente se les olvida.
está chido
bueno esta aplicación me parece buena pero no tiene los juegos como dice en los anuncios, me entristece que no tenga los juegos
Hola Alejandra:
Puedes acceder a los juegos después de la sesión diaria de 15 minutos de matemáticas.
No dudes en contactar con nuestro servicio de atención al cliente en [email protected] para cualquier duda adicional que tengas.
¡Un saludo!
Me encanta la página y me es muy útil
Gracias por la introducción que me dieron de las fracciones equivalentes
Mucha gracias profesor!!
Agradecida Profesor. Excelente su trabajo .
Me encantó. Una manera muy fácil y clara de aprender. Cosas que mis maestros no me aclaraban bien, pude aprender muchas cosas mas aquí. Muchas gracias creo que me va a ir bien en el examen
Muy bueno te entendí a ti más que a mi maestra
Muy claro y explícito, gracias.
Gracias Excelente explicacion, me ha ayudado mucho. tengo un niño en cuarto grado y le encanta la matemática pero esta parte le costaba .
Excelente la explicación para reafirmar conocimiento
Interesante muy buena me sacó las dudas que tenía
Agradecer por toda la información brindada ya que me ayudó mucho a resolver mis dudas gracias.
Muchas gracias a ti por tu comentario.
¡Un saludo!
Es interesante, es de una forma fácil de aprender.
Me gustó, lo encuentro práctico para aprender, veré si puedo tomarlo, gracias
Gracias por su colaboración. Son excelentes aportes a la didáctica del proceso educativo.
Esta bárbaro esto pero a mi me piden una fracción equivalente con un denominador 32 y no sé cómo lo realizo
Muchas gracias aprendí mucho
😊🤗😌😇
Hola les doy las gracias por su información la explicación es clara y sencilla, fácil de entender.
Soy una persona mayor y estoy haciendo la primaria. Cuando era joven no pude hacerla.
Cuando tengo que hacer los ejercicios, me ayudáis muchísimo. Muchas gracias.
¡Nos alegra que te podamos ayudar, Angelines! Te animo a que tu también pruebes el método Smartick. Gracias a que trabaja con inteligencia artificial, Smartick se adapta al nivel de conocimiento de cada alumno independientemente de su edad. Con sesiones de 15 minutos al día, podrás aprender matemáticas de una genial forma.
https://www.smartick.es
¡Un saludo!
Cool
Hola me gustó pero ¿por qué no ponen más problemas razonados?
Por favor, los necesito para mi hermana.
¡Hola Angie! En Smartick, además de nuestro método online de matemáticas y este blog, contamos con una página de recursos didácticos en la que podrás encontrar una gran variedad de ejercicios. ¡Aquí te dejo el link! Un saludo.
https://www.smartick.es/matematicas/recursos-didacticos.html
Hola gracias por tu explicación, la entendí.
Me ha servido mucho, gracias
¡Gracias por tu comentario, Gael!
Hola soy Yaneibis, sus clases soy muy especiales, los felicito.
me ayudó un montón gracias
mañana tengo examen seguro que sacaré un 10
¡Gracias por tu comentario Victoria! Mucha suerte en tu examen, seguro que lo haces genial.
Según un ejercicio planteado por Smartick, la fracciones 4/6 y 2/3 se pueden obtener simplificando a partir de 6/9. Sin embargo, según el planteamiento de este post, habría que dividir el numerador y el denominador entre 3, con lo que se obtiene únicamente 2/3 y no 4/6 como afirman en sus ejercicios y en un correo que les enviamos previamente, y en el que hacían referencia a estos posts para justificar la solución ¿Me podrían aclarar por qué consideran 4/6 como fracción simplificada obtenida a partir de 6/9?
Hola Fernando:
El post explica que para obtener fracciones simplificadas puedes dividir numerador y denominador por cualquier número, que no necesariamente es un número entero. Por ejemplo, si divides numerador y denominador de 6/9 entre 1,5 obtienes la fracción simplificada equivalente 4/6.
No hemos podido encontrar el correo al que haces referencia ya que la dirección que nos facilitas en este comentario no coincide con ninguna que tengamos registrada como usuario de Smartick.
Si quieres profundizar, por favor escribe a [email protected] y mis compañeros de atención a padres podrán solucionar todas tus dudas.
Muchas gracias y un saludo!
excelente explicación, gracias
Excelente, me ayudó mucho con la tarea de mi hijita.
No habíamos entendido las fracciones equivalentes pero aqui está muy bien explicado.
me ayudo bastante esta explicación ♥♥♥♥
Que chido
Muy bien me ayudó demasiado con mi tarea thanks
Me resultó útil
Excelente
Muchas gracias, me ha ayudado un montón 😉
Gracias fue muy útil para mis hermanos
Muchas gracias, me sirvió mucho para mi tarea.
Creo que si me sirvió muchísimo para mi tarea que ni palabras tengo para agradecer
Muy buena la explicación, mi hijo lo entendió correctamente, muchas gracias.
Muy bien este post, saqué 10 en la tarea.
la mejor página del mundo
Es superior me sirvió mucho en mi tarea
En realidad me está sirviendo!
Eres el amo de las matemáticas
SUPER GRACIAS TENÍA EXAMEN Y LO GANÉ GRACIAS
Gracias está bien explicado
Muchas gracias por crear esta página. Mi hija está encantada. Un saludo
me encanta muy buena técnica me parece excelente mil felicitaciones
muy bueno
genial mañana tengo evaluación y con esta explicación voy a salir bien
muy buena explicación lo necesitaba para recordar, buena metodología
me encantó gracias
Genial
Excelente.
Wow me encanta
Excelente explicación!!!!
Mil gracias por compartir!!!
Me encanta ahora voy a poder pasar el Exámen de Matemáticas
me ha ayudado a entenderlas muuuuuuuuuuuuuuchas gracias!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Muchas gracias es de mucha ayuda
Ok esta aplicación es geni al
gracias ahora si puedo hacerlo bien mil gracias al fin he entendido amo a smartick
me gusta Muy buen aporte me servirá de mucho tu información ya que lo manejas con ejemplos y me servirá para enseñar o dar como referencia. Gracias por el aporte.
muy bien me encantan las fracciones
A mi tambien me gustan las fracciones Dalisner Mendoza
a mi también me gusta
tengo un examen hoy y creo que lo voy a pasar ¡¡¡¡¡¡gracias!!!!!!!!
esto me ayudó mucho la verdad se los recomiendo
Puedes multiplicar (o dividir) por el número que quieras, siempre que sea el mismo en numerador y denominador. Es decir 1/2 es equivalente a 2/4 (hemos multiplicado por 2 numerador y denominador), equivalente a 3/6 (multiplicado por 3 numerador y denominador), equivalente a 8/16 (multiplicado por 8 numerador y denominador) y así todas las equivalencias que quieras!
hola buen dia ,,,muchas gracias en lo particular muy buena su pagina ,,,lo unico que no me quedo claro fue como se elige el numero por el cual se multiplicara para sacar equivalencias
Hola Lulu,
Puedes multiplicar (o dividir) por el número que quieras, siempre que sea el mismo en numerador y denominador. Es decir 1/2 es equivalente a 2/4 (hemos multiplicado por 2 numerador y denominador), equivalente a 3/6 (multiplicado por 3 numerador y denominador), equivalente a 8/16 (multiplicado por 8 numerador y denominador) y así todas las equivalencias que quieras!
Hola
Excelente muchas gracias por tu comentario yo ya puedo pasar mis tareas y examen y aprendí muy Rápido y gracias por tu comentario muchas grasiasssssssssssssss
Mil gracias pues con sus ejemplos mi nena y yo logramos entender las fracciones equivalentes. Gracias por su gran aporte.
ME PARECEN MUY INTERESANTES, NECESITO ENTENDER PARA EXPLICARLE
A MIS NIÑOS TENGO UN NIÑO Y UNA NIÑA EN 4 Y 5 DE PRIMARIA
Gracias me ayudó mucho!!
Pues muchas gracias por ayudar
a mí me ayudó muchísimo, más de lo que esperé
Me ayudo mucho! Gracias! ✖➗
Amo me podrían decir el resultado de 12/15+12/15+12/15=xfa
Hola Adamaris:
En este caso las 3 fracciones tienen el mismo denominador, por lo que es muy fácil calcular el resultado.
me estan dejando de tarea q ilumine 1/5 en unos cuadritos como le ago si son 60 cuadritos como se donde es 1/5
ME PUEDES DECIR EL RESULTADO DE LA FRACCION 4/6 + 3/2 + 4/12
Que fracción es
Por ejemplo
3 séptimas y 2 tercero
Qué fracción seria
es bueno saber para que aprendamos
verdad que aprender es divertido
por favor dime la fraccion equivalente de 3/4 con denominador 36.por faa
felicidades por explicar de manera muy entendible
no entendi la amplificacion
ayudenme es que en simplificacion entendi pero no muy bien en amplificacion por que no se por que en el ejemplo todos se multiplicavan por 2X2 y despues se multiplico por 3X3 alguien me podria decir por que se hiso eso
me puede decir como soluciono este fracciones (1/3+2/4)-2/6
hola tengo una duda por que la primera figura tiene un medio si primero como estan las otras figuras tienen que multiplicar
por ejemplo
2x 1
2x 2
es igual a 2×1=2 y 2×2=4
esa era mi duda gracias y ogala me envien su opinion
esta bien pero deberías poner el ejemplo 4/10
estoy confundido quiero sabes 2/6 de 12 no entiendo nada.. porfa
Hola Jose Daniel!
Para practicar y aprender fácilmente fracciones y todos los temas de matemáticas de primaria, te invitamos a registrarte gratis en http://www.smartick.es, allí podrás practicar y repasar.
Un saludo!
No te entendi nada me dices la equivalencia de 2/5 con dibujo please
estoy confundido quiero sabes 1/2 de 12 no entiendo nada.. porfa
pues 10 – 5 : 48 esque yo no seeeeee
Es muy rapido y muy bueno se los recomiendo gracias
muy rapido de encontrar gracias y muy bien
Es facil de encontrar y dibertido muchas gracias
es un buen ejercicio
Excelente información. Muy sencilla y facil de entender.
muchas gracias fue la única pagina fácil de entender y comprensible te decía todo de las equivalencias me gusto
muchas gracias por la información aunque no era la que necesitaba pero aun así muchas gracias.
me gusta y si era la que andaba buscando gracias voy a ver mas resultados tuyos gracias de nuevo
Muy buen aporte. Aunque ya lo sabía porque me gustan mucho las fracciones, pero me servirá de mucho tu información ya que lo manejas con ejemplos y me servirá para enseñar o dar como referencia. Gracias por el aporte.
Soy una de tantas madres que piensa que los niñ@s de primaria tienen que aprender antes a usar las tablas que la tablet, ya que las matemáticas es una actividad que tenemos que usar todos los días, sobre todo las amas de casa, unas más y otras menos.
Por eso vuelvo a decir que hay que aprenderlas desde pequeñito, poco a poquito.
Tiene razón un buen aporte
Me encanta la información y la página
Muchas gracias los amo muchísimo
Excelente.