En el post de hoy vamos a conocer cómo realizaban una multiplicación en la antigüedad en distintas culturas.
Te ayudará a comprender mejor el funcionamiento del algoritmo clásico de la multiplicación, que seguro que has practicado bastante, pero que quizá no comprendes del todo por qué es así.
Veremos los métodos Chino y Egipcio, y para entenderlos mejor, resolveremos la multiplicación 31 x 42 con ayuda de ellos.
Método Chino de multiplicación
Los Chinos hacían las multiplicaciones con varillas de bambú, disponiéndolas de manera horizontal y vertical, como veremos el ejemplo.
Veamos cómo puedes multiplicar 31 x 42 mediante este método.
En primer lugar, coloca:
- 3 rayas horizontales separadas la misma distancia y, un poquito más separada, 1 raya horizontal más.
- 4 rayas verticales separadas la misma distancia y, un poquito más separada, 2 rayas verticales más.
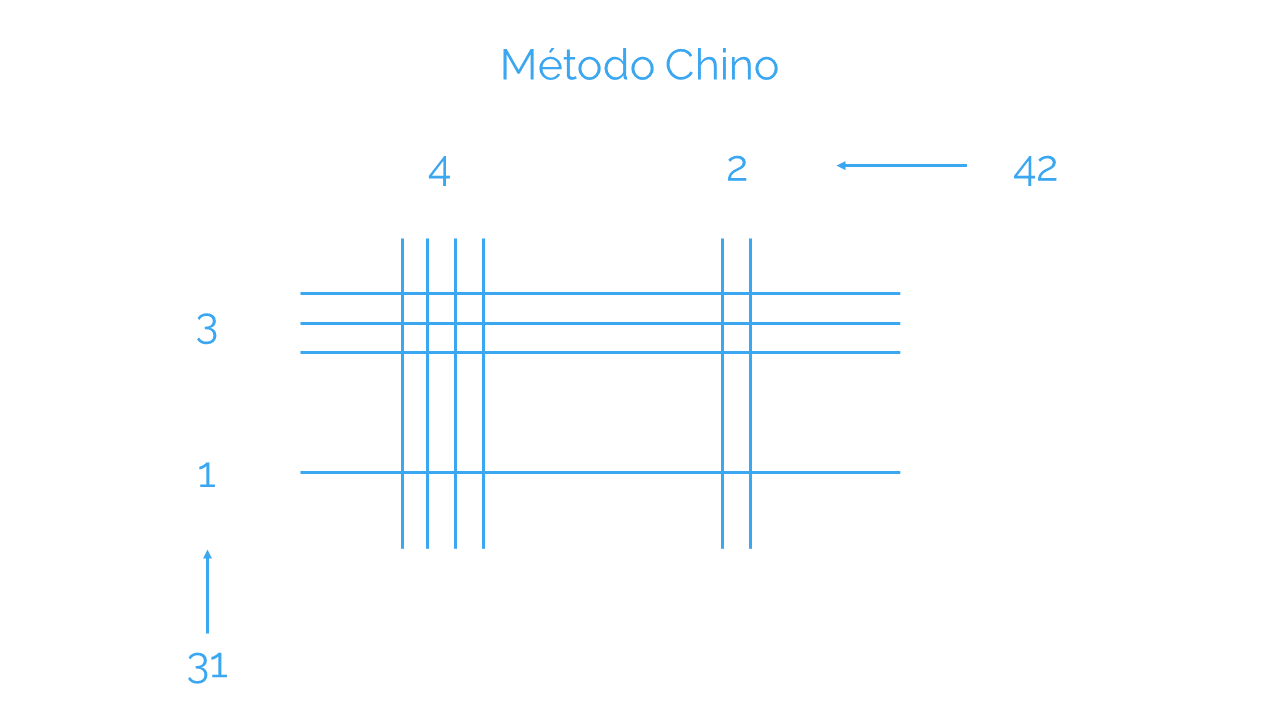Luego cuenta los cruces de cada par de rayas, distinguiendo si son las correspondientes a unidades o decenas:
- Cruzando rayas de unidades, obtienes las unidades del resultado (ya que el producto de unidades devuelve unidades).
- Cruzando rayas de unidades y decenas, obtienes las decenas del resultado (ya que el producto de unidades y decenas devuelve decenas).
- Cruzando rayas de decenas, obtienes las centenas del resultado (ya que el producto de decenas devuelve centenas).
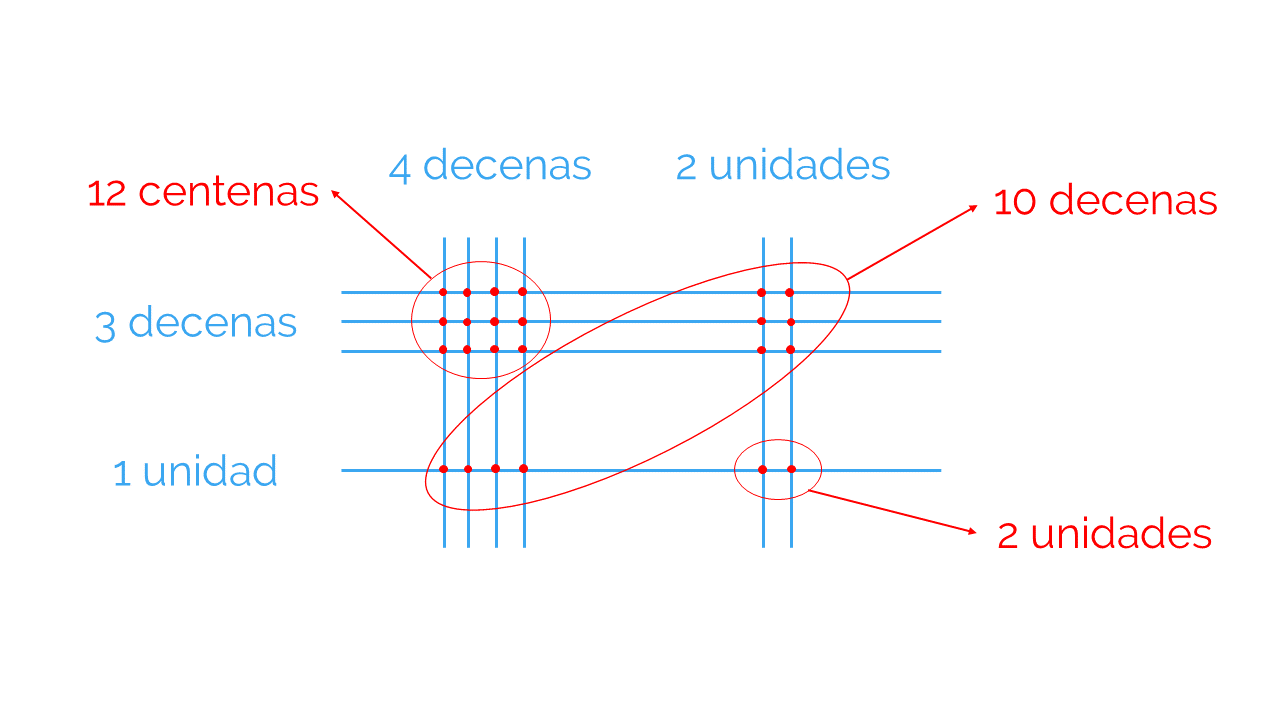Ahora, puedes recopilar todo lo que has obtenido, que será el resultado de la multiplicación 31 x 42:
- 2 unidades.
- 10 decenas, que es lo mismo que 1 centena.
- 12 centenas, que sumado a la centena de las 10 decenas son 13 centenas. Estas 13 centenas son 1 unidad de millar y 3 centenas.
Habrás obtenido:
1 unidad de millar, 3 centenas y 2 unidades; es decir, 1.302
Así que has obtenido que 31 x 42 = 1.302
Método Egipcio de multiplicación
Los Egipcios hacían las multiplicaciones por un método que consiste en descomponer la multiplicación en una serie de sumas, realizando dobles de uno de los factores de la multiplicación (consiguiendo ponerlo en potencias de 2).
Veamos cómo puedes multiplicar 31 x 42 mediante este método.
Coloca primero 1 y 31, y ve realizando dobles de las 2 cantidades, de la siguiente manera:
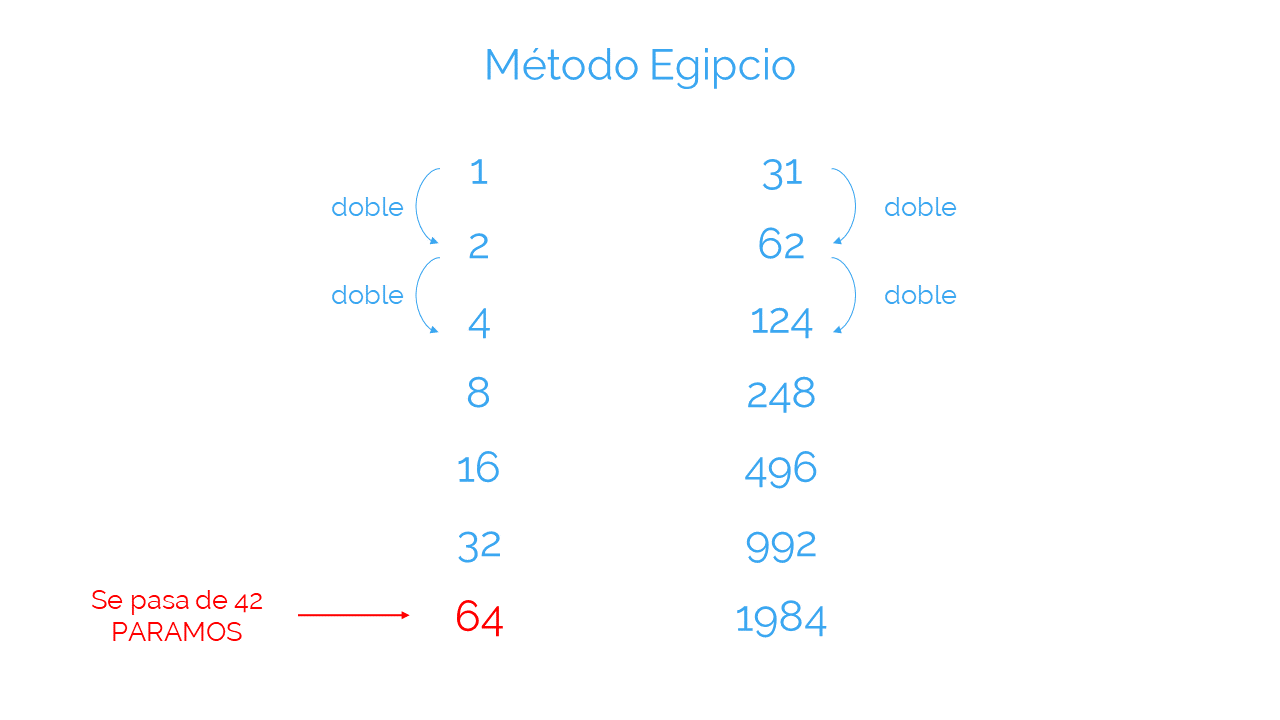
Habrás obtenido así distintas multiplicaciones de 31 por potencias de 2.
Ahora lo importante es que busques las que te ayuden a resolver la multiplicación 31 x 42. Para ello, no tienes más que buscar las potencias de 2 que suman 42:
32 + 8 + 2 = 42
Habrás conseguido así descomponer 31 x 42 en sumas que ya has calculado antes fácilmente:
31 x 42 = 31 x (2 + 8 +32) = 31 x 2 + 31 x 8 + 31 x 32 = 62 + 248 + 992 = 310 + 992 = 1.302
Así que habrás obtenido también que 31 x 42 = 1.302
Espero que estos métodos para realizar multiplicaciones te hayan ayudado a comprender mejor el funcionamiento de la multiplicación y te animes a compartirlos con tus amigos. Puedes revisar también esta entrada de nuestro blog sobre multiplicaciones con métodos alternativos: el método Ruso y el método Hindú.
Y ya sabes, si quieres aprender y practicar más matemáticas, regístrate en Smartick y pruébalo gratis.
Para seguir aprendiendo:
- Cómo realizar multiplicaciones con un modelo de área
- Multiplicaciones: aprende a hacerlas, ejemplos y más
- Multiplicaciones con métodos alternativos. Método Ruso y método Hindú
- Multiplicación: el algoritmo con la ayuda de bloques
- Multiplicar por dos y por tres cifras
Forma parte del equipo de desarrollo de contenidos de Smartick.
Amante de la naturaleza, el yoga y el baile.
- Valor absoluto de un número - 28/10/2019
- Cálculo de áreas de polígonos - 16/09/2019
- Potencias y su representación con regletas - 08/07/2019
Excelente material. Soy docente y me es muy útil.
El juego es un excelente método de aprendisaje y más aún de las matemáticas.
Hola desde El Salvador, muy buen aporte. No hay por qué hacer difícil las matemáticas.