En este post vamos a ver cuándo podemos utilizar una regla de 3 como herramienta para resolver una problema.
La regla de 3 es uno de los fenómenos matemáticos más aplicables, conocidos y útiles, sobre todo por su combinación de simplicidad y eficiencia. Resuelven problemas en los que hay relaciones multiplicativas entre sus magnitudes. Eso sí, para aplicar una regla de 3 tienes que tener muy claro qué relación se da entre las magnitudes que intervienen, si ésta es de proporcionalidad directa o inversa… o si no hay relación de proporcionalidad.
Supón que nos ponen el siguiente problema:
Si en dos cajas iguales hay un total de 6 cámaras de vídeo, ¿cuántas cámaras de vídeo habrá en tres cajas?
Es una de esas situaciones en las que podemos aplicar la regla de 3. ¿Por qué?, porque si se dobla el número de cajas se dobla el de cámaras; si se triplica el número de cajas, también el de cámaras… de hecho, eso es exactamente en lo que se apoya la regla de 3. Vamos a hacer una reducción a la unidad, si el número de cajas fuese la mitad (una) el de cámaras también sería la mitad: tres cámaras.
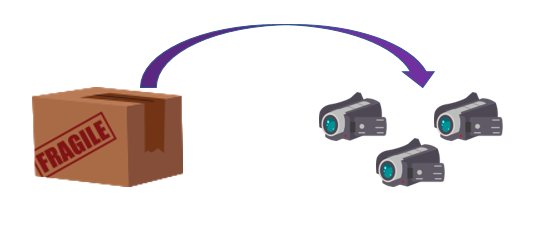
Ahora, sabiendo esto podemos terminar el problema:
¿Cuántas cámaras habrá en tres cajas (iguales)?
Esta situación solo la podemos resolver porque sabemos la cantidad de cámaras que hay en cada caja y por tanto aplicamos esta relación a las tres cajas.
«Si en una caja hay 3 cámaras, en 3 cajas habrá el mismo contenido que en una caja multiplicado por 3»
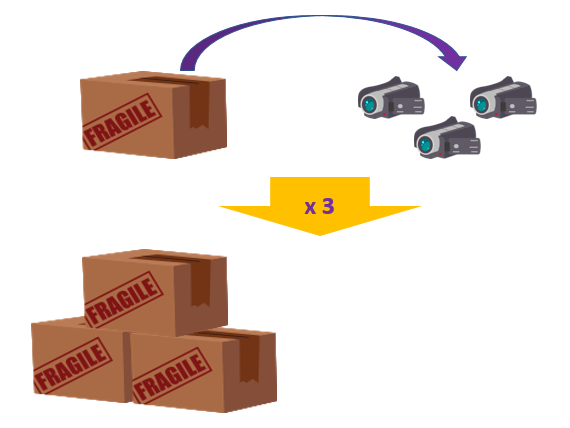
Este es el razonamiento en el que se apoya la regla de 3.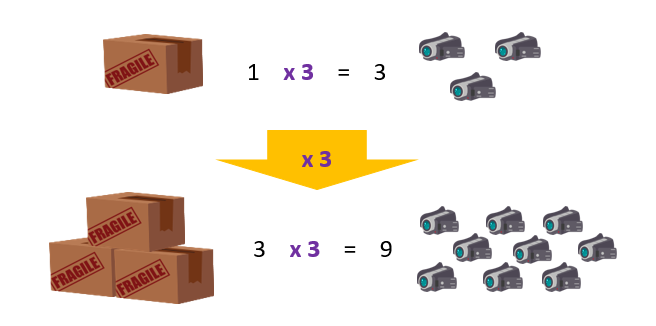 
Pero, ¿hemos utilizado de verdad una regla de 3?
La regla de 3 es un procedimiento con el que a partir de 3 números que están en relación de proporcionalidad directa (o inversa) hallamos un cuarto. Nosotros teníamos 3 números y hemos hallado un cuarto, por lo que -técnicamente- la respuesta es sí.
Lo que pasa es que normalmente hablamos de regla de 3 a la receta esa de «este por este entre este». Esta regla se suele aplicar sin comprensión y que solo funciona si elegimos cuidadosamente los números que multiplicamos y que dividimos.
El procedimiento que hemos utilizado aquí es el de la reducción a la unidad, calcular el número de cámaras que habrá en una única caja y luego multiplicar por el número de cajas. Nos hemos adueñado del procedimiento, lo hemos hecho nuestro. Esto siempre será mejor que aplicar procedimientos sin comprensión.
Ahora ya entiendes qué es una regla de 3. Si quieres ver más ejemplos y ejercicios con los que puedes practicar, pincha en los siguientes enlaces y accederás a otros posts en los que se profundiza más en la aplicación y los usos de la regla de tres.
Y si quieres aprender muchas más matemáticas de primaria, regístrate en Smartick y pruébalo gratis.
Para seguir aprendiendo:
- Proporcionalidad inversa, regla de tres inversa
- Regla de 3 simple directa e inversa
- Regla de 3: resumen de entradas
- Regla de 3 compuesta: cuándo se utiliza y algunos problemas
- La doble recta numérica. Qué es y cómo se utiliza
Maestro de vocación y acción, forma parte del departamento de pedagogía de Smartick y trata de aportar la experiencia que ha ganado curso tras curso en el aula.
Cree ciegamente que no hay mejor forma de enseñar algo a un niño que a través de un manipulativo físico o digital.
“Aprender el qué a través del cómo”.
Deseo repasar la regla de tres simple. Después avanzaré.
Hola Hugo. Te dejo este enlace a nuestro blog donde explicamos la regla de tres simple directa e inversa. Espero que te sea de ayuda.
https://www.smartick.es/blog/matematicas/algebra/regla-de-3-simple/
Un saludo