En este post vamos hablar del marco teórico del Método Singapur, el cual gira en torno a la resolución de problemas matemáticos.
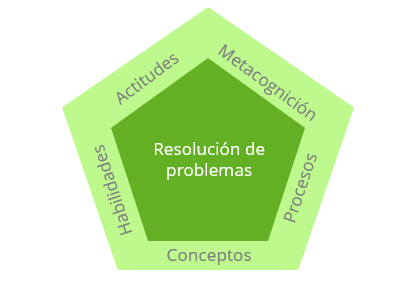
Conceptos
El Método Singapur agrupa los conceptos matemáticos en 6 secciones:
- Números
- Álgebra
- Geometría
- Estadística
- Probabilidad
- Análisis
Estas categorías de contenido están íntimamente conectadas y son interdependientes. En las diferentes etapas del aprendizaje, así como en los diferentes programas, la amplitud y profundidad del contenido varían.
Habilidades
El Método Singapur trabaja las destrezas de:
- Cálculo numérico
- Manipulación algebraica
- Visualización espacial
- Análisis de datos
- Medición
- Uso de herramientas matemáticas
- Estimación
- Además, también desarrolla la capacidad de usar hojas de cálculo y software que faciliten el aprendizaje de las matemáticas.
Todas estas habilidades no se enseñan de forma meramente instrumental, sino desde la comprensión y la justificación.
Metacognición
La metacognición, o el pensamiento sobre el pensamiento, se refiere a la conciencia y a la capacidad de controlar, regular y evaluar los procesos del pensamiento. En particular, alude a la selección y al uso de estrategias de resolución de problemas.
Para desarrollar la conciencia y las estrategias metacognitivas, los estudiantes que siguen el método Singapur deben enfrentarse a la resolución de problemas no rutinarios y abiertos. Asimismo, también han de discutir sus soluciones, pensar en voz alta y reflexionar sobre lo que están haciendo. Todo ello al tiempo que mantienen un registro actualizado sobre cómo marchan las cosas.
Actitudes
Las actitudes consisten en los aspectos afectivos del aprendizaje de las matemáticas, tales como:
- Creencias sobre las matemáticas y su utilidad
- Interés y disfrute en el aprendizaje de las matemáticas
- Apreciación de la belleza de las matemáticas
- Confianza en el uso de las matemáticas
- Perseverancia en la resolución de problemas
Son muy consciente que las actitudes de los estudiantes hacia las matemáticas están moldeadas por sus experiencias de aprendizaje. Hacer que el aprendizaje sea divertido, significativo y relevante ayuda en gran medida a inculcar actitudes positivas hacia las materias.
Procesos
En el Método Singapur los procesos matemáticos incluyen:
- El razonamiento matemático, que es la capacidad de analizar situaciones matemáticas y construir argumentos lógicos. Es un hábito mental que se puede desarrollar a través de la aplicación de las matemáticas en diferentes contextos.
- Comunicación, que es la capacidad de usar el lenguaje matemático para expresar ideas de manera precisa, concisa y lógica.
- Las conexiones, que son la capacidad de ver y establecer vínculos entre las ideas matemáticas, entre las matemáticas y otras materias, y entre las matemáticas y el mundo real. Todo esto ayuda a los estudiantes a entender realmente lo que aprenden en matemáticas.
- El modelado matemático, que es el proceso de formular un modelo matemático para representar y resolver problemas del mundo real. A través de modelos matemáticos, los estudiantes aprenden a lidiar con la ambigüedad, a hacer conexiones, a seleccionar y aplicar los conceptos y las habilidades matemáticas adecuadas, a identificar suposiciones y reflexionar sobre las soluciones de problemas y, también, a tomar decisiones informadas basadas en datos dados o recopilados.
- Las habilidades de pensamiento, esto es, la capacidad de clasificar, comparar y analizar los problemas de forma global.
- El pensamiento heurístico, es decir, el conjunto de procedimientos que los estudiantes utilizan para abordar un problema cuya solución no es obvia. Se incluye el uso de la representación (por ejemplo, dibujar un diagrama), de la conjetura (por ejemplo, prueba y error, hacer suposiciones), el recorrer el proceso (por ejemplo, trabajar hacia atrás) y el introducir cambios en el problema (por ejemplo, simplificando el problema, considerando casos especiales).
Referencias:
- Smartick aterriza en Singapur, uno de los sistemas educativos más exigentes.
- Singapur: Metas, objetivos y diseño de su Plan de Estudios
Para seguir aprendiendo:
- Singapur: Metas, objetivos y diseño de su Plan de Estudios
- Singapur: Experiencias de aprendizaje
- Barras de Singapur aplicadas a la resolución de problemas
- Problemas matemáticos para niños de Primaria: actividades divertidas y educativas
- Singapur: Principios de enseñanza y fases de aprendizaje
- Resolución de problemas de matemáticas - 24/02/2020
- Las cinco etapas de la práctica deliberada - 06/01/2020
- La auto explicación en el proceso de aprendizaje - 25/11/2019








Me parece interesante, apliquemos en el aula.
muy bonito e interesante