En el post de hoy vamos a explicar los ejercicios de resta de fracciones. Además, veremos algunas de las actividades de resta de fracciones que hacen los alumnos en Smartick.
En un post anterior del blog explicamos cómo resolver una resta de fracciones. Puedes entrar a revisarlo antes de seguir leyendo.
Para hacer algunos ejercicios de resta de fracciones hay que saber cómo calcular el mínimo común múltiplo (mcm) entre diferentes números.
¿Ya sabes hacer el mínimo común múltiplo? Entonces continuamos.
Índice
Fracciones con el mismo denominador
Pasos para restar fracciones con el mismo denominador
Podemos restar fracciones sin hacer ningún otro paso intermedio cuando tienen el mismo denominador, solo tienes que:
- Escribir el mismo denominador que tienen las fracciones en la fracción resultante.
- Restar los numeradores y escribir el resultado en la fracción resultante.
Ejemplos
- \(\frac{7}{3}\) – \(\frac{2}{3}\) = \(\frac{5}{3}\)
- \(\frac{10}{5}\) – \(\frac{2}{5}\) = \(\frac{8}{5}\)
Ejercicios resueltos
Ahora, vamos a ver un par de actividades que los niños y niñas hacen en Smartick sobre resta de fracciones con el mismo denominador.
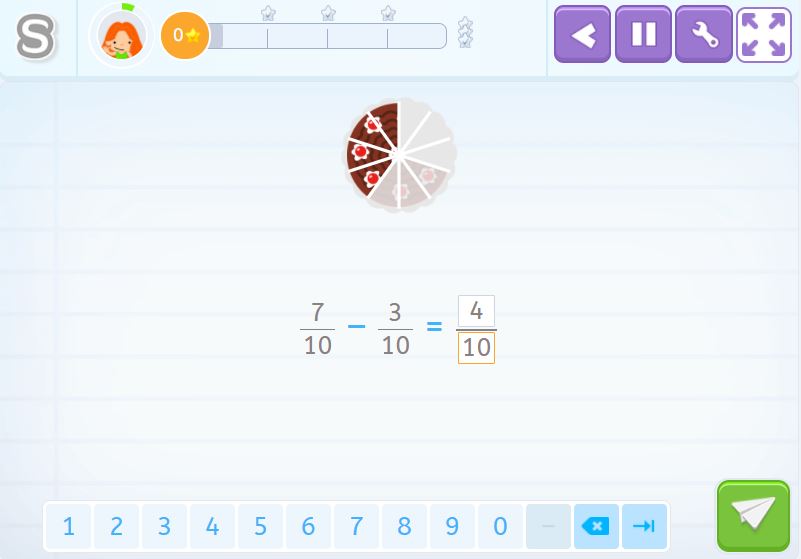
Como puedes ver, la tarta es un apoyo visual que te puede ayudar a realizar la resta de fracciones. Está dividida en 10 partes iguales de las cuales al final solo nos quedamos con 4 trozos de tarta.
\(\frac{7}{10}\) – \(\frac{3}{10}\) = \(\frac{4}{10}\) trozos de tarta.
Por cierto que la fracción de antes \(\frac{4}{10}\) tiene numerador y denominador pares, se puede simplificar si lo haces veras que \(\frac{4}{10}\) de tarta representa lo mismo que \(\frac{2}{5}\) de tarta, aunque los trozos de tarta no se puedan volver a pegar una vez cortados.
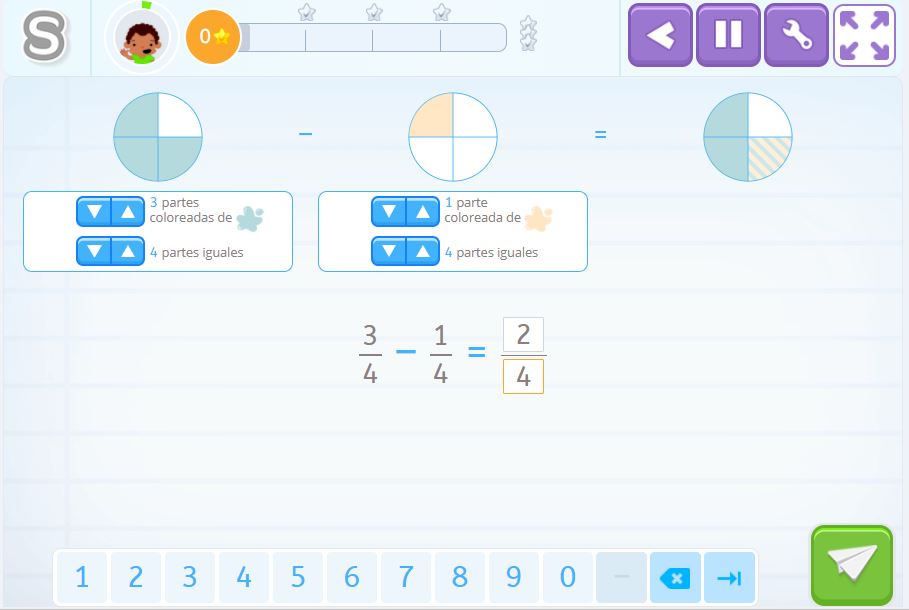
En esta actividad, te puedes ayudar de los círculos para representar las fracciones. Primero, tenemos que dividir en 4 partes iguales los dos círculos y después colorear en uno 3 partes y en otro solo una. Vemos que el círculo que nos sale tiene solamente dos partes coloreadas de azul.
\(\frac{3}{4}\) – \(\frac{1}{4}\) = \(\frac{2}{4}\) partes del círculo coloreadas, o sea, la mitad.
Fracciones con distinto denominador
Podemos encontrarnos con:
- Una resta de fracciones más complejas. Este tipo de fracciones son las que tienen distinto denominador y un denominador no es múltiplo del otro. Por ejemplo: \(\frac{5}{6}\) – \(\frac{7}{13}\)
- Una resta de fracciones más sencillas. Este tipo de fracciones son las que tienen distinto denominador siendo un denominador múltiplo del otro. Por ejemplo: \(\frac{5}{6}\) – \(\frac{7}{12}\) (12 es múltiplo de 6).
En los dos casos, tenemos que hacer que las fracciones que vamos a restar tengan el mismo denominador porque si no, no podemos hacer la resta.
Pasos para restar fracciones cuando un denominador no es múltiplo del otro
Para hacer la resta de fracciones más complejas tenemos que hacer que las fracciones tengan el mismo denominador, ese denominador tiene que ser múltiplo de los dos denominadores. Nos valdría cualquier múltiplo común, pero recomendamos utilizar el mínimo común múltiplo, los pasos a seguir son:
- Hallar el mínimo común múltiplo de los denominadores de las fracciones.
- Escribir nuevas fracciones equivalentes a las iniciales con el mínimo común múltiplo como denominador de ellas.
- Las fracciones resultantes ya tienen el mismo denominador, así que restaremos los numeradores y escribiremos el resultado en la fracción resultante.
Ejemplo 1
\(\frac{2}{3}\) – \(\frac{3}{5}\)
Lo primero que vamos a hacer el hallar el mínimo común múltiplo entre los denominadores de las fracciones:
m.c.m. (3, 5) = 15
Ahora escribimos las fracciones equivalentes a las anteriores con el denominador igual a 15:
\(\frac{2}{3}\) = \(\frac{?}{15}\)
Para saber el número del numerador, tendremos que multiplicar el numerador (2) por el mismo número que se haya multiplicado el denominador.
Para pasar de 3 a 15 hemos multiplicado por 5. Por tanto el numerador también lo multiplicamos por 5.
\(\frac{2}{3}\) = \(\frac{10}{15}\)
Hacemos lo mismo con la otra fracción:
\(\frac{3}{5}\) = \(\frac{?}{15}\)
El denominador se ha multiplicado por 3, entonces el numerador también lo tenemos que multiplicar por 3:
\(\frac{3}{5}\) = \(\frac{9}{15}\)
Ahora que las fracciones tienen el mismo denominador las podemos restar:
\(\frac{10}{15}\) – \(\frac{9}{15}\) = \(\frac{1}{15}\)
Ejemplo 2
\(\frac{5}{6}\) – \(\frac{3}{10}\)
El mínimo común múltiplo entre 6 y 10 es 30.
Hallamos las fracciones equivalentes:
\(\frac{5}{6}\) = \(\frac{?}{30}\)
El denominador se ha multiplicado por 5 por lo tanto el numerador también hay que multiplicarlo por 5:
\(\frac{5}{6}\) = \(\frac{25}{30}\)
Lo hacemos con la otra fracción:
\(\frac{3}{10}\) = \(\frac{?}{30}\)
El denominador se ha multiplicado por 3 por lo tanto el numerador también hay que multiplicarlo por 3:
\(\frac{3}{10}\) = \(\frac{9}{30}\)
Por último, restamos las fracciones:
\(\frac{25}{30}\) – \(\frac{9}{30}\) = \(\frac{16}{30}\)
Esta última fracción también se puede simplificar:
\(\frac{16}{30}\) = \(\frac{8}{15}\)
Pasos para restar fracciones cuando un denominador es múltiplo del otro
Podríamos hacer el mínimo común múltiplo entre los denominadores, pero vamos a ver otra forma de hacer la resta de fracciones más sencillas que solo vale para este tipo de fracciones, los pasos a seguir son:
- Encontrar la fracción equivalente de la fracción que tiene como denominador un divisor del denominador de la otra fracción, para que los dos denominadores de las fracciones sean iguales.
- Las fracciones resultantes ya tienen el mismo denominador, así que restaremos los numeradores y escribiremos el resultado en la fracción resultante.
Ejemplo 1
\(\frac{5}{6}\) – \(\frac{7}{12}\)
La fracción equivalente a \(\frac{5}{6}\) es \(\frac{10}{12}\), hemos multiplicado numerador y denominador por 2.
Ahora ya tenemos las dos fracciones con el mismo denominador, 12:
\(\frac{10}{12}\) – \(\frac{7}{12}\)
Entonces, el resultado de la resta es:
\(\frac{10}{12}\) – \(\frac{7}{12}\) = \(\frac{3}{12}\)
Ejemplo 2
También podemos buscar esta fracción equivalente de forma visual e intuitiva. Vamos a verlo con un ejemplo resuelto de Smartick:
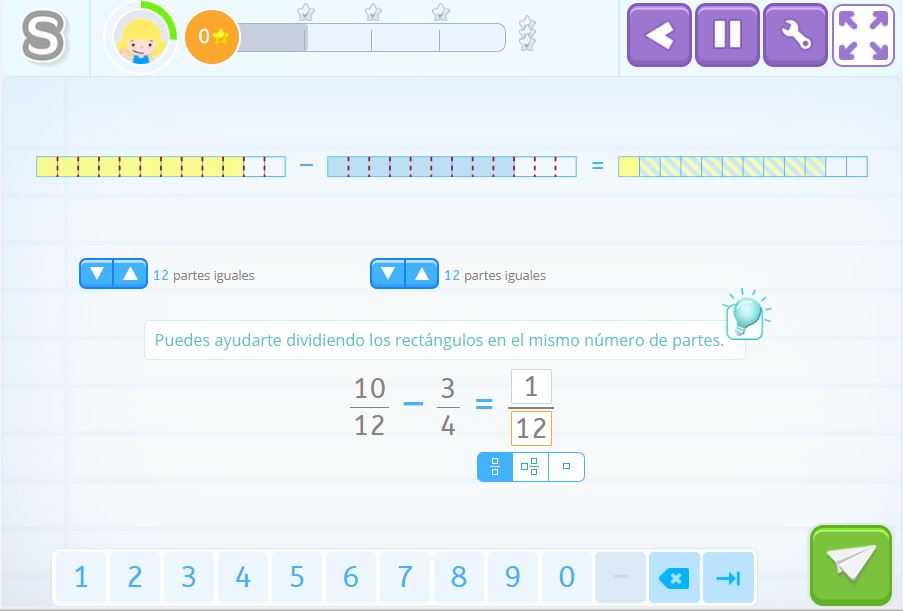
En esta actividad te puedes ayudar de las barras para saber el resultado de la resta de las fracciones, simplemente hay que poner el mismo número de partes en las que están divididas las dos barras, en este caso se dividen en 12 partes iguales. Después de dividir las barras en el mismo número de partes es fácil ver, de forma gráfica el resultado de la resta, \(\frac{1}{12}\), que como ves está representado en la barra final (solo hay coloreado un cuadrado y la barra está dividida en 12 partes).
Utilizando las barras también podemos ver que la fracción equivalente a \(\frac{3}{4}\) es \(\frac{9}{12}\), y la resta de las fracciones quedaría: \(\frac{10}{12}\) – \(\frac{9}{12}\) = \(\frac{1}{12}\).
Ejercicios resueltos
Y para terminar, vamos a ver varios ejemplos de las actividades que se hacen en Smartick sobre resta de fracciones con distinto denominador.
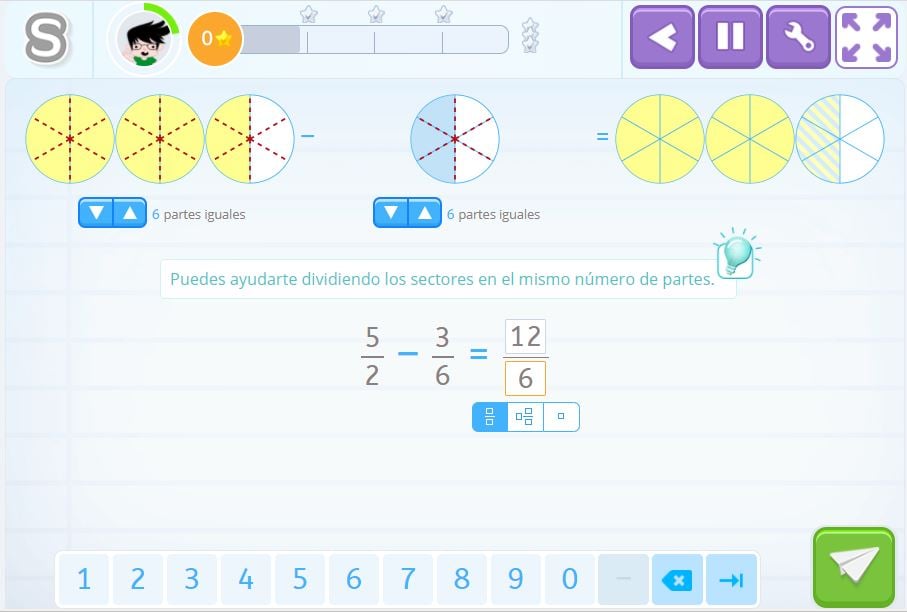
Esta vez utilizamos círculos para representar las fracciones. Te puedes ayudar de los círculos para saber el resultado de la fracción, simplemente hay que poner el mismo número de partes en los dos círculos, en este caso se dividen en 6 partes iguales.
Como ves, el resultado de la resta de fracciones es \(\frac{12}{6}\). Puedes comprobar si lo has hecho bien mirando el resultado de los círculos. Dos círculos completos.
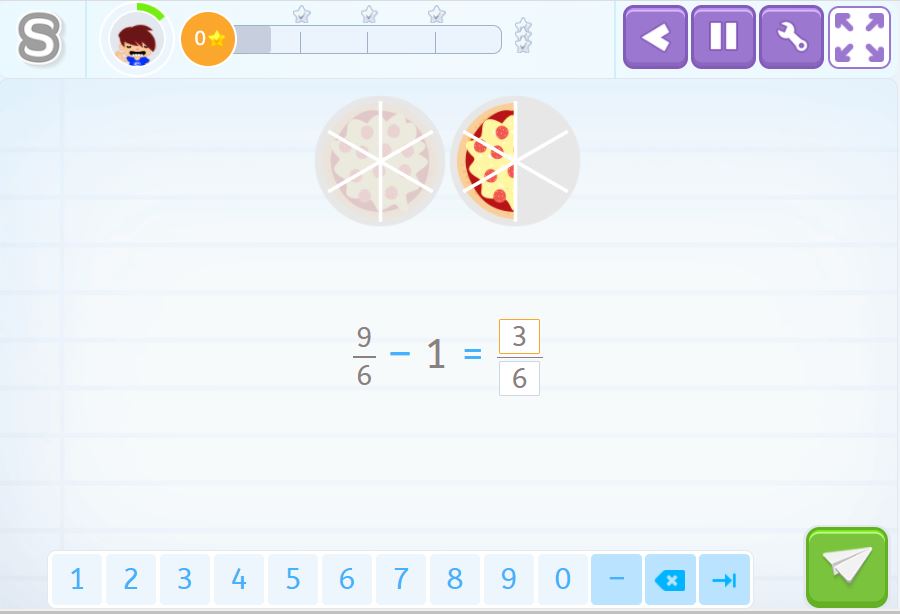
Esta actividad es muy fácil, aquí nos podemos ayudar de las pizzas dibujadas para saber el resultado de la resta de fracciones.
Tienes dos opciones para resolver el ejercicio:
- Hacer el m.c.m. de 6 y 1 que es 6.
- Sacar la fracción equivalente a 1, que es \(\frac{6}{6}\).
¿Has aprendido a hacer ejercicios de resta de fracciones?
Ahora te propongo los siguientes ejercicios de resta de fracciones para que demuestres que lo sabes.
- \(\frac{8}{5}\) – \(\frac{3}{5}\)
- \(\frac{3}{2}\) – \(\frac{2}{3}\)
- \(\frac{7}{4}\) – \(\frac{7}{8}\)
- \(\frac{5}{6}\) – \(\frac{1}{15}\)
Las soluciones son:
- \(\frac{5}{5}=1\)
- \(\frac{5}{6}\)
- \(\frac{7}{8}\)
- \(\frac{23}{30}\)
Vídeo para entender las fracciones equivalentes
El siguiente vídeo te puede ayudar a entender mejor qué son las fracciones equivalentes para facilitarte la resta de fracciones con distinto denominador.
Es uno de nuestros tutoriales interactivos convertido en vídeo, por lo que deja de ser interactivo 🙁. Aún así tiene la gran ventaja de que se puede visualizar tantas veces como sea necesario y compartir. Si quieres acceder a los tutoriales interactivos de verdad, puedes hacerlo registrándote en Smartick, el método online de aprendizaje de matemáticas para niños de 4 a 14 años.
Y, si quieres seguir aprendiendo muchas más matemáticas de primaria, adaptadas a tu nivel, regístrate en Smartick y pruébalo gratis.
Para seguir aprendiendo:
- Cómo resolver una resta de fracciones
- Suma y resta de fracciones
- Clasificación de fracciones: propias, impropias y unitarias
- Cómo resolver una suma de fracciones
- División de fracciones. Diferentes métodos








La información es bastante entendible.
muchas gracias 😁👍 me ayudaron mucho 😘😍
Muchas gracias por tu comentario Dismar, esperamos que te haya servido de ayuda nuestro post. ¡Un saludo! 😊
Me interesan los materiales para 6º grado.
Hola me encantó muchísimo y también me ayudó.
Buenos días quiero averiguar el valor de las clases
Hola Alejandra:
Smartick es un método online que se adapta al nivel de cada niño. En sesiones de 15 minutos diarios pueden aprender con programas de matemáticas, lectura, programación y pensamiento crítico. Dependiendo del programa que se tenga contratado.
El coste depende del número de niños que registres, la duración del compromiso (mensual, trimestral o anual) y la divisa con que pagues, tenemos alumnos en más de 100 países.
Te recomiendo que te registres en http://www.smartick.com como tutor y a tus hijos como alumnos. Ofrecemos un periodo de prueba gratuito, sin ningún tipo de compromiso, para que podáis conocer Smartick.
En la web de padres, a la que accedes con tu correo de registro y contraseña, puedes revisar las tarifas que aplican en tu caso.
Paso tu comentario a mis compañeras de atención pedagógica que contactarán contigo en el correo que nos has facilitado.
Puedes comunicarte directamente con ellas en [email protected]
¡Un saludo!
Quiero saber el precio ya que aparecia gratis y después aparece que solo es gratis por 7 días !!!
Hola Wuamer:
Como indicamos en el post, la prueba es gratis.
El precio de Smartick pasados esos días depende de los programas que contrates (matemáticas, lectura o ambos), el número de alumnos y la divisa con la que pagues, estamos en más de 100 países.
Te recomiendo que registres a tus hijos en el periodo de prueba gratuito, sin ningún tipo de compromiso, y accedas en la web de padres, con tu correo de registro y contraseña, a las tarifas que aplican en tu caso.
Puedes contactar en todo momento con mis compañeras de atención al cliente en [email protected] para resolver cualquier duda adicional que puedas tener.
Les envío este comentario del blog para que te escriban al correo que nos has facilitado y te expliquen bien todo.
¡Un saludo!
QUE COSTO TIENE CADA SECCION
Hola Samuel:
El registro en Smartick es gratuito y damos 7 días de prueba sin ningún tipo de compromiso. El coste depende del número de alumnos que contraten, la duración de la suscripción (mensual, trimestral o anual) y el número de programas.
Paso tu comentario a mis compañeras de atención al cliente que intentarán contactar contigo en el correo que nos facilitas en este comentario. Puedes escribirlas en todo momento a [email protected]
¡Un saludo!