A veces nos puede interesar conocer si un número es divisible entre otro sin tener que realizar la división entera. Esto es especialmente útil cuando trabajamos con números muy grandes que requerirían de muchísimo tiempo para completar los cálculos. Si quieres refrescar los criterios de divisibilidad, puedes echar un ojo a esta entrada anterior de nuestro blog.
Sin embargo, en este post vamos a ir más allá, pues explicaremos la razón por la que los criterios de divisibilidad funcionan. Así que… ¡Vamos con ello!
La idea fundamental de la divisibilidad es la noción de resto. Cuando dividimos, partimos de un conjunto que tiene una cantidad de elementos (dividendo) y los vamos agrupando formando subconjuntos más pequeños, todos ellos con la misma cantidad de elementos (divisor). El resto son los elementos que «sobran» cuando ya no podemos seguir haciendo agrupaciones. Puedes revisar la división aquí. Así, el resto siempre es menor que el divisor, pues de lo contrario podríamos seguir haciendo agrupaciones. Por ejemplo, si estamos dividiendo entre 3, el resto solo puede ser 0, 1 o 2.
Los restos de dividir entre cualquier número cumplen siempre algunas propiedades Entre ellas, nos van a interesar dos: si a y b son dos números enteros cualesquiera, entonces
- resto de ( a + b ) = resto de ( ( resto de a ) + ( resto de b ) )
- resto de ( a x b ) = resto de ( ( resto de a ) x ( resto de b ) )
¡Comprueba que se cumplen!
Por otro lado, cuando tenemos un número, siempre podemos escribirlo de acuerdo a su representación decimal. Por ejemplo, si tenemos un número de 2 cifras, AB, podemos expresarlo como
AB = A x 10 + B
Echando mano de las propiedades de los restos, tenemos que…
resto de ( AB ) = resto de ( ( resto de A ) x ( resto de 10 ) + ( resto de B ) )
Lo que sucede ahora es que, si sabemos el resto de cada una de las cifras (A, B) y el resto de 10, podemos conseguir el resto del número original. Y, además, podemos ir haciéndolo por orden, de izquierda a derecha, en la expresión anterior. Primero usamos el resto de A,
( resto de A )
luego multiplicamos por el resto de 10,
( resto de A ) x ( resto de 10 )
y después sumamos el resto de B,
( resto de A ) x ( resto de 10 ) + ( resto de B ) .
Si el número que nos ha salido fuese mayor que el divisor, nos quedaríamos con el resto de este nuevo número.
Para entenderlo mejor, vamos a hacer un grafo que nos permita hacer lo anterior de forma visual con un número concreto. Por ejemplo, el resto que resulta de dividir entre 7. Podíamos haber elegido otro, pero… ¡nos gusta el 7!
Los posibles restos son entonces 0, 1, 2, 3, 4, 5, y 6. Y, además, se van repitiendo en ese orden. En efecto, el resto de 7 entre 7 es 0, el de 8 entre 7 es 1, el de 9 entre 7 es 2…
Primero colocaremos los posibles restos en los vértices de un heptágono (figura de 7 lados). A continuación, los unimos por flechas azules orientadas en el sentido en que se van sucediendo los restos. Ahora, unimos con flechas moradas cada uno de los restos con el resto del número que resulta de multiplicarlo por 10. Por ejemplo, el 3 lo unimos con una flecha morada con 2 pues 3 x 10 = 30 y el resto de dividir 30 entre 7 es 2. Así, hemos obtenido el siguiente grafo:
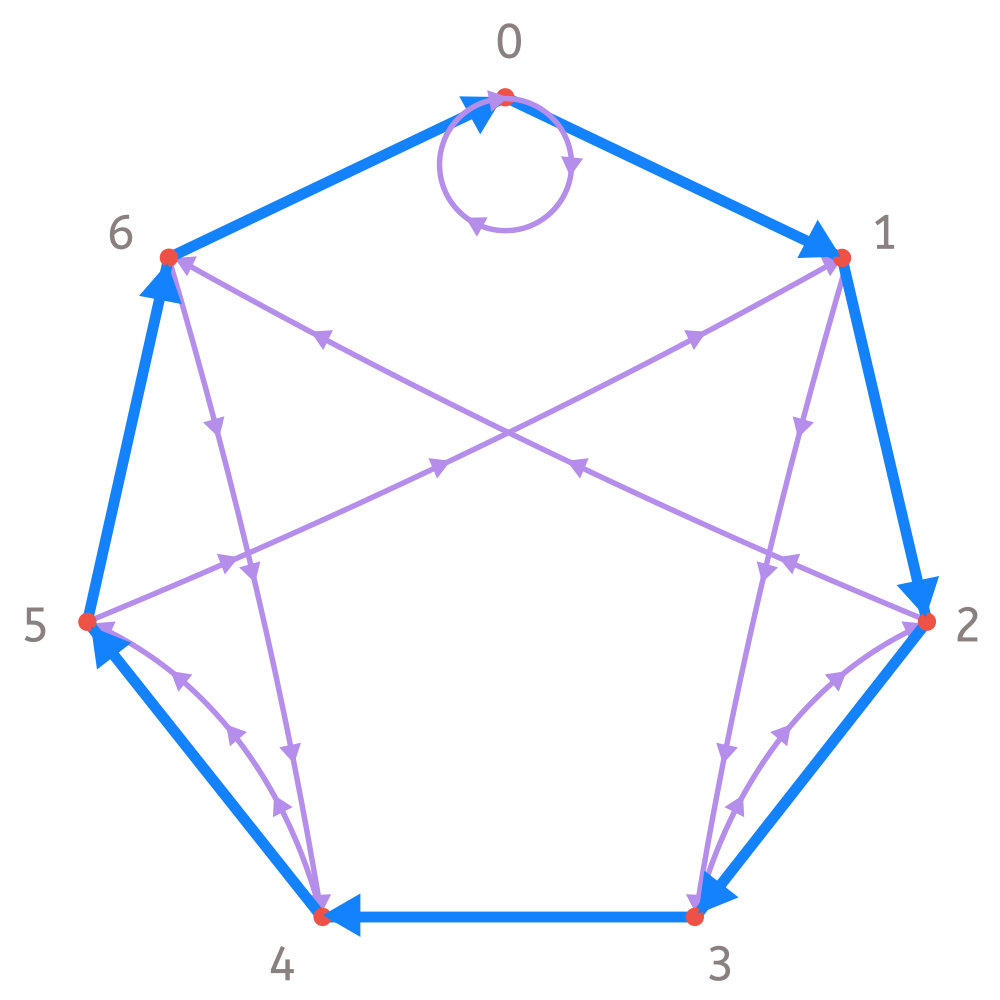
El método anterior se traduce en que, partiendo desde el 0, tenemos que recorrer tantas flechas azules como indique la primera cifra (leyendo por desde la izquierda) del número y después una morada. A continuación, hacemos lo mismo con la siguiente cifra.
Por ejemplo, vamos a ver si el número 91 es divisible entre 7. Primero recorremos 9 flechas azules, partiendo desde el 0.
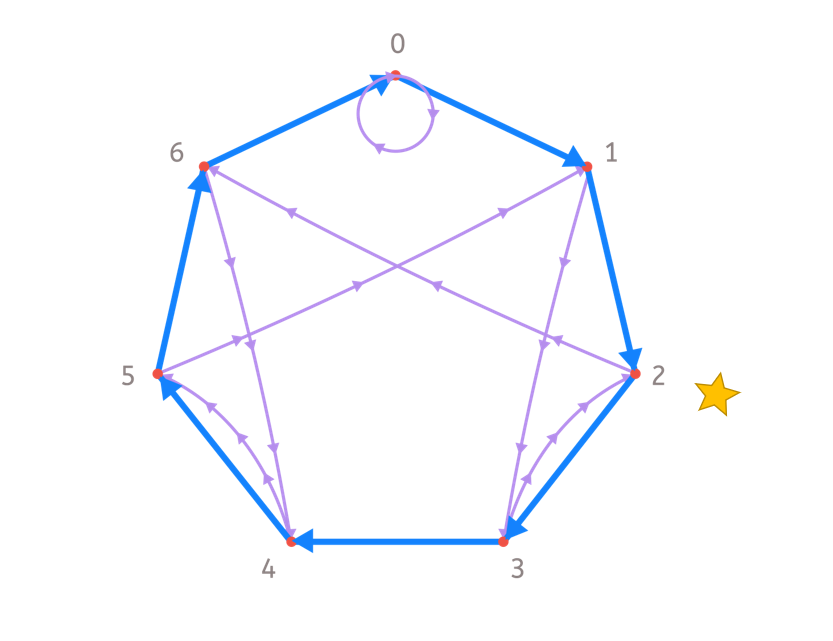
Ahora, seguimos una flecha morada y vamos a parar al 6.
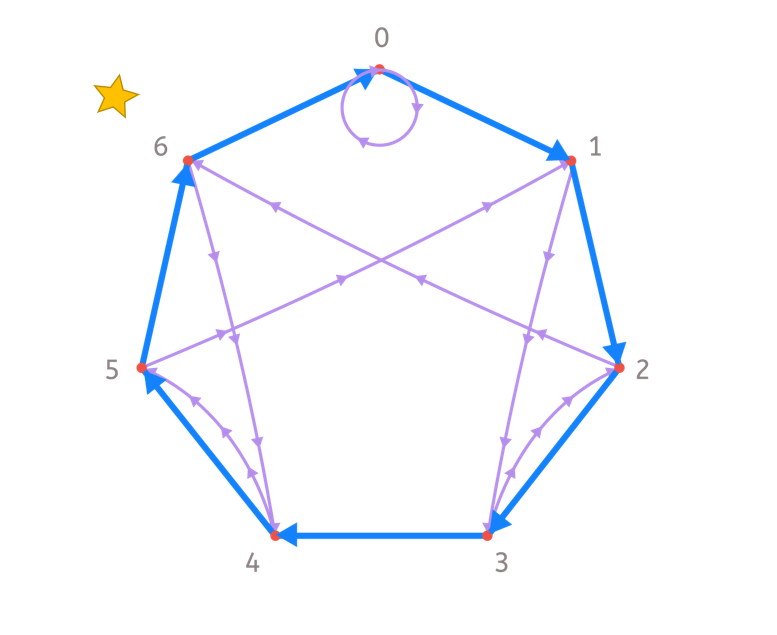
Como la siguiente cifra del número es un 1, recorremos 1 flecha azul y llegamos al 0. ¡Ojo! ¡Si la cifra es la última, ya no tenemos que recorrer la flecha morada! Así llegamos a…
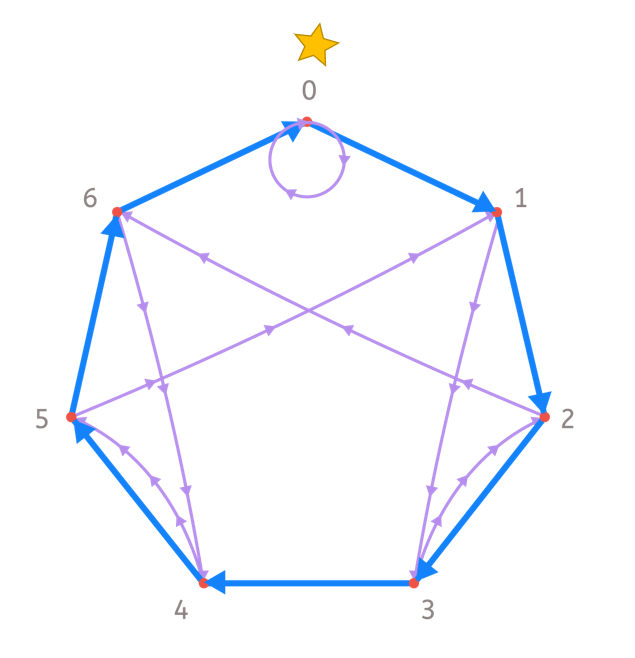
Como hemos acabado en el 0, sabemos que el resto de dividir 91 es 0. O dicho de otra forma, que 91 es divisible entre 7. ¡Compruébalo!
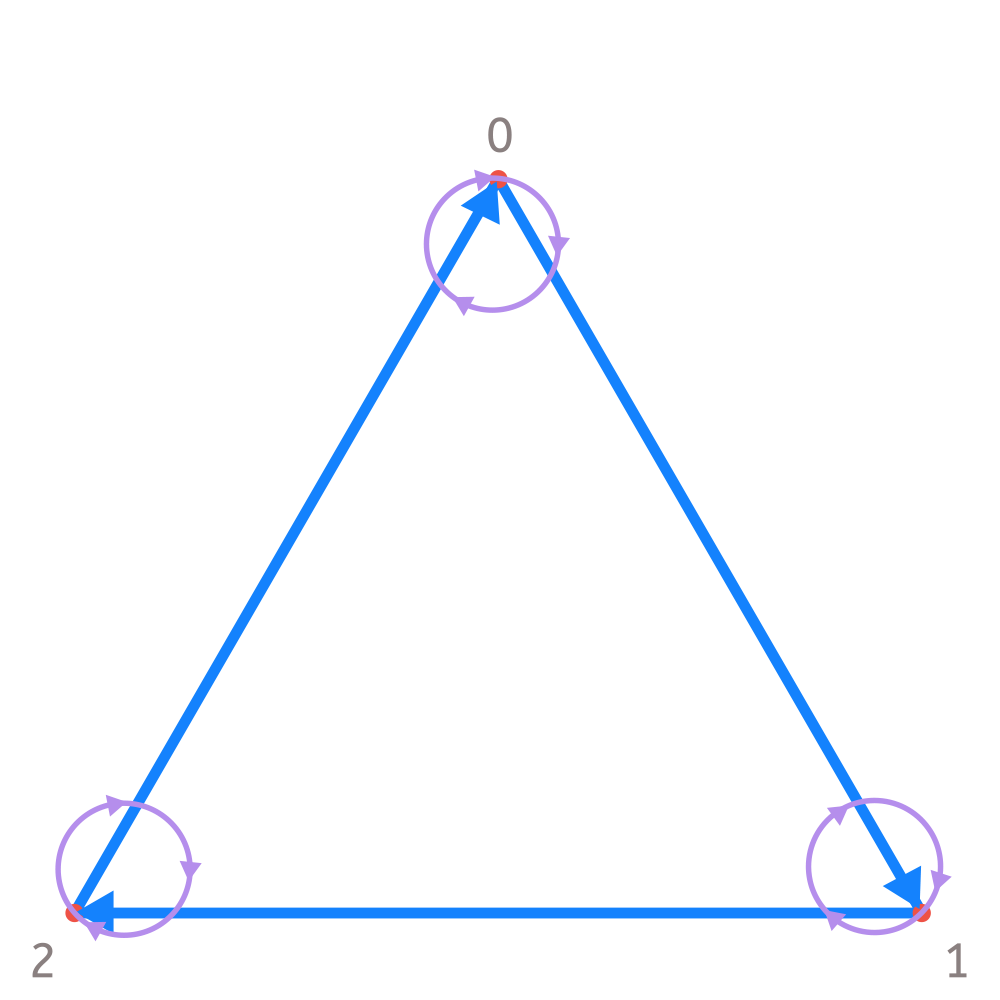
Esta forma de ver los criterios de divisibilidad sirve para números de más cifras. Solo tienes que seguir correctamente el camino de flechas azules y moradas para saber si es divisible entre 7. Además, puedes hacer tu propio grafo para el número que quieras y así obtendrás tu propio criterio de divisibilidad. A continuación, puedes ver los del número 3. En este caso utilizamos un triángulo porque tiene 3 lados. Fíjate en que las flechas moradas van siempre al mismo vértice. Eso quiere decir que realmente lo que importa es dónde acabas si das tantos pasos como la suma de todas las cifras. ¿Te recuerda eso al criterio de divisibilidad del 3? 😉
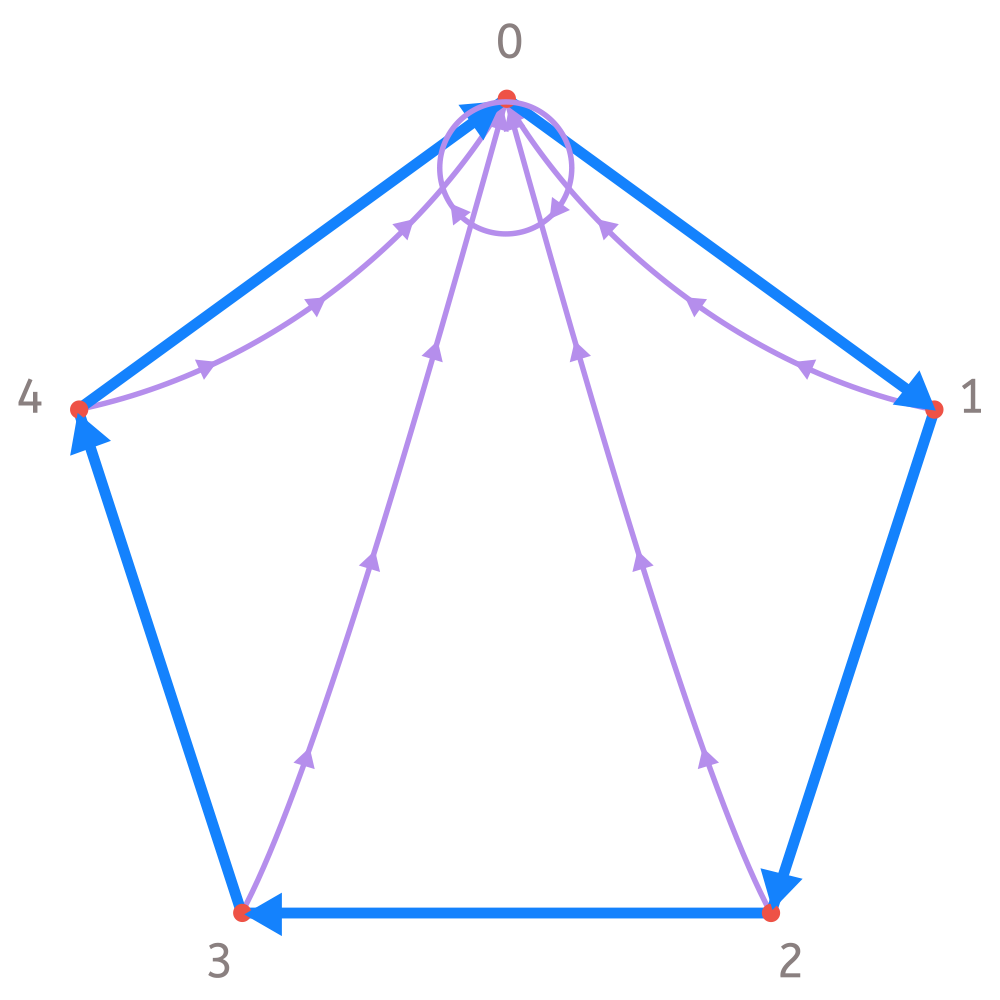
Te voy a mostrar también el grafo del número 5 (con un pentágono, figura de 5 lados). Todas las flechas moradas van a parar al 0 pues cualquier número multiplicado por 10 es divisible entre 5. Así, lo único que importa es lo que ocurre con la última cifra. Solo si esta es 5 o 10 acabamos en el 0. ¡El criterio de divisibilidad del 5!
¿A qué esperas para construir el criterio de divisibilidad de, por ejemplo, el número 13? 😀
Espero que hayas ampliado tu conocimiento sobre los criterios de divisibilidad y que ahora sepas por qué funcionan. Si quieres seguir aprendiendo cosas como esta… Únete a la comunidad Smartick. ¡Pruébalo gratis!
Para seguir aprendiendo:
- Divisibilidad del 7
- Criterios de divisibilidad del 7 y del 13
- Criterios de divisibilidad del 6 con ejemplos
- Criterio de divisibilidad del 5
- Criterios de divisibilidad del 6, del 8 y del 12
- Propiedades de las potencias - 13/04/2020
- El porqué de los criterios de divisibilidad - 02/03/2020
- Por qué son importantes los ejemplos en la enseñanza de las matemáticas - 27/01/2020







