Ceros en el cociente de una división
02 mayo 2016
En este post vamos a ver la razón por la cual se ponen ceros en el cociente de una división cuando se dividen números enteros.
Más adelante haremos otra entrada explicando cuándo se ponen ceros en el cociente de una división al dividir números con decimales.
Este post se debe a una duda de uno de nuestros lectores del blog. A esta persona, como a muchas otras, le enseñaron que si, al resolver una división, se encontraba este tipo de situación:
El dividendo resultante es menor que el divisor (5<9)
No podía aplicar aquello de,«buscar un cociente (del 1 al 9) que, al multiplicarlo por el divisor, dé un resultado igual o menor que el dividendo».
Para esta situación se debe seguir la consigna de «añadir un cero al cociente, bajar la siguiente cifra del dividendo y continuar dividiendo».
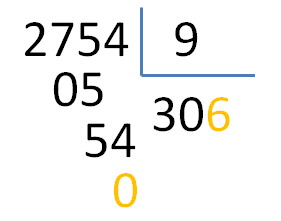
Tras hacer eso y seguir dividiendo vemos que todo encaja y que el resultado obtenido es el correcto.
La división es correcta (2574 / 9 = 306 y de resto 0)
Hasta aquí todo bien, pero su pregunta era debida a que no entendía de dónde salía aquel cero que se añadía al cociente. Ya que en el colegio se lo habían enseñado como una regla nemotécnica, que debía aplicar solo en este tipo de situaciones, sin explicarle el motivo.
No le encontraba el sentido lógico a dicha «aparición mágica de ceros», y nos lo preguntó a nosotros.
Ahora que ya he situado la duda, procederé a explicarla.
Ese cero que se pone en el cociente, no es más que el único número que «al multiplicarlo por el divisor da como resultado un número menor que el dividendo»
Multiplicamos el divisor (9) por un número (0) que de como resultado el dividendo (5) o menor. [9 x 0 = 0 ; 0 es menor que 5] Luego restamos el número obtenido al dividendo [5 – 0 = 5]
Ahora sí, bajamos la siguiente cifra de dividendo y seguimos con nuestra división.
Multiplicamos el divisor (9) por un número (6) que dé como resultado el dividendo (54) o menor. [9 x 6 = 54 ; 54 es igual que 54; nos da resto 0]
Al final lo que estamos haciendo es seguir las instrucciones de resolución de una división para cualquier circunstancia. No es necesario aplicar ninguna «regla especial» si no incluir al cero entre los posibles valores que pueden multiplicar al divisor.
Dicho de otra forma, en el colegio intentaban agilizar el proceso con un automatismo que ahorra un paso pero rompe con la dinámica de resolución y por tanto la complica. Es mejor normalizar esta situación como una más «si el dividendo es menor que el divisor, multiplico este por cero y obtengo un número menor que ambos…«
Está bien que cuando el alumno tenga interiorizado todo el proceso de la división y haya desarrollado la soltura adecuada a la hora de resolver divisiones de una o dos cifras en el divisor (incluyendo ceros en el cociente), sepa que hay un «atajo» que pueden usar o no. Pero sólo después de que entienda el motivo de los ceros en el cociente de una división.
Esperamos que con este post os haya quedado claro el «mágico lugar del que proceden los ceros».
Y si quieres practicar muchas más matemáticas, entra en Smartick y pruébalo gratis.
26 Comentarios
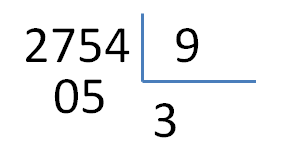
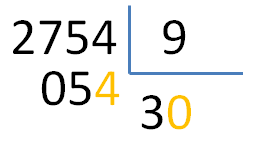
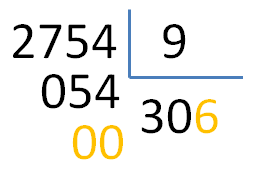
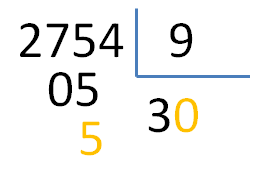
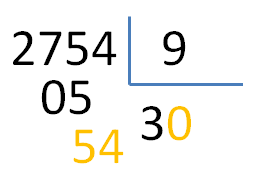
Congratulaciones al profesor y al grupo que conforma este propositivo equipo de comprensión y fomento del conocimiento matemático. Ciertamente muchas lagunas cognitivas deben ser abordadas y pedagógicamente argumentadas con pertinencia en tiempo y manera o modo. Éxitos a todos en la noble aventura del saber y bien hacer el bien.
Me ayudó mucho la razón y uso del cero en las divisiones.
Muy claro y conciso.
Gracias.
¡Muchas gracias Ángeles!
Muchas gracias, no sabia como explicárselo a mi hija, ahora entiendo el porqué se coloca el cero en el cociente
Que Dios lo bendiga.
Hola Mary:
Si quieres que tu hija aprenda sola, con contenidos adaptados a su nivel y ritmo de aprendizaje, te recomiendo que te registres en Smartick y probéis los 7 días de prueba gratuita sin ningún tipo de compromiso.
Estamos a tu disposición en [email protected] para resolver cualquier duda que tengas.
¡Un saludo!
Gracias por compattir tu conocimiento
me ha sido de gran ayuda para explicar a los pequeños de la casa
Muchas gracias, hasta ahora lo entiendo y me doy cuenta de lo importante que es conocer el por qué se hace. Ahora yo les estoy enseñando a mis hijos y agradezco esta excelente información
Muchas gracias señor César, todo lo que planteó en este post es muy verdadero, jamás me habían explicado porque poner el cero en las divisiones. O si me lo dijeron no me acordaba. De igual manera gracias por aclarar esa duda una y mil gracias.
Excelente explicación! Muchas gracias
GRACIAS ESTOY HACIENDO TAREA Y ME AYUDÓ MUCHO
Muchas gracias César por la explicación y sugerencia en el modo de enseñar a los niños (as) que se inician en esta operación aritmética
¡Muchas gracias por tu comentario!
Muchas gracias por fin encontré una explicación clara. ¡¡Muchos éxitos!!
¡Gracias por tu comentario, Verónica!
Excelente trabajo hacen ustedes. Me ha ayudado mucho. Mil gracias.
¡Muchas gracias, Rafael! ¿Conoces nuestro método Smartick? No dudes en visitar nuestra página web. Ofrecemos un periodo de prueba gratuito, sin ningún tipo de compromiso, para que puedas utilizarlo intensamente antes de decidir.
https://www.smartick.es
Hola amigos de Smartick muchas gracias por la información es una gran ayuda su página. Qué bueno que haya personas como ustedes que compartan su ayuda soy docente y por muchos años esto fue un dolor de cabeza para mi hoy me han aclarado la duda que tenia yo lo resolvía mecánicamente. Ya puedo explicar a mis alumnos gracias
Nos ha sido de mucha ayuda. Lo hemos entendido perfecto. Gracias
Gracias por la explicación
Muchas gracias
Gracias con tu explicación entendimos.
Excelente página, nos está ayudando bastante!
Gracias me ayudó mucho tu explicación para los peques en mi casa
¡Muchas gracias!
Muy útil y bien explicado.
Te amo.
hola entendí esta actividad !muchas gracias¡