Coordenadas cartesianas: qué son, cómo funcionan y para qué sirven

En el post de hoy vas a aprender todo sobre coordenadas cartesianas: qué son, para qué sirven, cómo funcionan… Además, verás unos cuantos ejemplos de los ejercicios de coordenadas que los alumnos de Smartick hacen en sus sesiones diarias de matemáticas personalizadas.

¿Qué son las coordenadas cartesianas?

Cuando jugamos a los barcos, decimos una letra para la posición vertical y un número para la horizontal, y así tratamos de encontrar los barcos de nuestro rival. Cuando jugamos a los barcos estamos utilizando coordenadas cartesianas.

Coordenadas cartesianas es el nombre que se da al sistema para localizar un punto en el espacio. En las enseñanzas obligatorias trabajamos las coordenadas cartesianas en espacios de dos dimensiones, los planos, pero podemos dar coordenadas cartesianas en espacios de tres o más dimensiones. El «apellido» de las coordenadas cartesianas es un homenaje al filósofo y matemático de René Descartes.

Un sistema de coordenadas cartesianas está formado por dos rectas perpendiculares graduadas a las que llamamos ejes de coordenadas. Se suele nombrar como X el eje horizontal e Y al eje vertical. Estos dos ejes se cortan en un punto al que se le denomina origen de coordenadas, O.

Otro nombre que reciben los ejes de coordenadas es el de abscisas para el eje X (horizontal),  y ordenadas para el eje Y (vertical).

Cuando queremos saber cuáles son las coordenadas de un determinado punto (al que nombramos generalmente con letras mayúsculas P, Q, R… o A, B, C…  debemos tener en cuenta que se colocan así:

(abscisa, ordenada)

Así que si decimos que el punto P tiene coordenadas (3,5) estamos diciendo que se encuentra sobre el 3 del eje horizontal a altura 5.

¿Cómo funcionan las coordenadas cartesianas?

Si queremos localizar algo en un plano necesitamos:

• Una medida horizontal: izquierda-derecha. A la que llamamos X.

• Una medida vertical: arriba-abajo. A la que llamamos Y.

• Un punto de referencia desde el que empezar a medir: el origen. Lo llamamos origen de coordenadas, O.

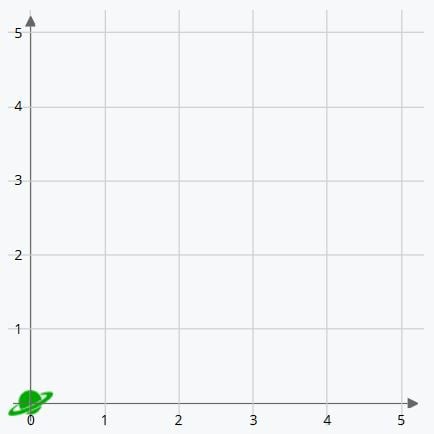
Llamamos origen de coordenadas al punto O, donde está el planeta verde en la imagen de arriba, porque es el punto del que parten las líneas que marcan los dos ejes de coordenadas.

Empecemos con la dirección horizontal, izquierda-derecha. Como ves, los números empiezan en el origen. El primer valor es cero y van creciendo a medida que nos desplazamos hacia la derecha. Éste es el eje X de coordenadas, y cuanto mayor sea su valor, más a la derecha se localizará el punto. Así, 4 en el eje X está 4 posiciones a la derecha del origen.

También tenemos una dirección vertical, arriba-abajo. Igual que en el eje X, los valores empiezan en el origen con cero y van creciendo a medida que nos desplazamos hacia arriba. Éste es el eje Y de coordenadas. Cuanto mayor su valor, más arriba. Por ejemplo, 5 está cinco posiciones por encima del origen.

En el juego de ponerle la cola al burro necesitamos que nos digan cuánto a la derecha o a la izquierda se encuentra y, además, cómo de arriba o abajo está. Para localizar un punto en un plano necesitamos exactamente lo mismo. Dos números: uno en el eje X y otro en el eje Y. Así la posición queda definida, el primer número indica cuánto a la derecha se encuentra y el segundo cómo de arriba está. Normalmente estos números van separados por una coma y rodeados por paréntesis de la siguiente manera: (X,Y).

Ejemplos de coordenadas

El origen siempre está situado en las coordenadas (0,0). Es decir, está lo más a la izquierda y abajo posible. O es un punto especial, desde él comienzan los ejes de coordenadas y está “0 posiciones a la derecha y 0 posiciones arriba”. Éste es el punto desde el que se empieza a contar. Entonces (0,3) estaría 0 posiciones a la derecha y 3 arriba. Y (5,0) 5 posiciones a la derecha y 0 arriba.

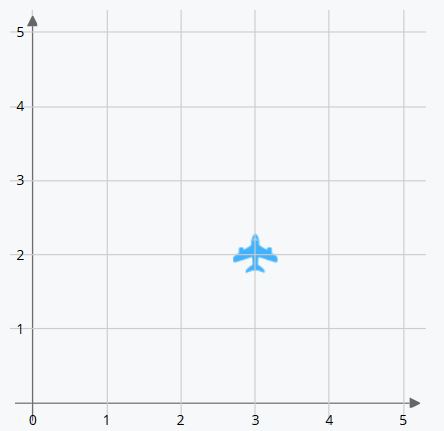
Por ejemplo, un avión azul en las coordenadas (3,2) ¿Dónde se localizaría?

La primera coordenada nos indica la posición en el eje X. Hay que contar 3 posiciones desde el origen hacia la derecha. Y la segunda coordenada la posición del eje Y, contar 2 posiciones hacia arriba. Así situamos al avión azul 3 posiciones a la derecha del origen y 2 hacia arriba.

Ahora vamos a ver el ejemplo inverso. Colocamos el objeto y debemos indicar en qué coordenadas se encuentra. ¿En qué coordenadas está el árbol amarillo?

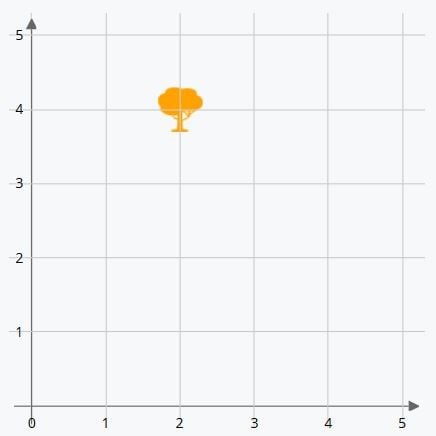
Podemos ver que está situado dos posiciones a la derecha del origen (eje X) y 4 hacia arriba (eje Y). Primero se escribe la coordenada del eje X y luego la del eje Y.

El árbol amarillo está en las coordenadas (2,4).

Para qué sirven las coordenadas

Además de su uso en matemáticas, la utilidad cotidiana de las coordenadas cartesianas suele ser localizar sitios en los mapas. Los planos suelen estar divididos en sectores con ejes horizontales y verticales. El mapa puede ser de unas pocas calles, una ciudad o del globo terráqueo entero. Así se puede saber dónde vive un amigo de tu barrio, dónde te encuentras en la visita a una ciudad o dónde está la atracción a la que quieres ir en el parque de atracciones.

Otro contexto en el que encontramos frecuentemente planos y coordenadas es cuando ponemos el GPS. Pero cuidado, el GPS no da coordenadas cartesianas aunque en la pantalla del móvil veamos un plano, la tierra es esférica y el GPS se geolocaliza utilizando satélites sobre la superficie de la tierra. Los valores que utiliza el GPS son los de la latitud (lo mucho o poco que estemos al norte o al sur del ecuador), y la longitud (que mide si estamos al este o al oeste del meridiano de Greenwich). Puedes consultar nuestro post sobre qué es un ángulo y como se mide.

Cuadrantes

Hasta ahora hemos considerado solo la parte del plano en el que tanto el eje X, abcisas (horizontales), como el eje Y, ordenadas (verticales) son números positivos, pero perfectamente pueden ser negativos. Si lo necesitas puedes consultar nuestra entrada sobre cómo ubicar los diferentes números en la recta numérica, porque lo que tenemos cuando usamos coordenadas cartesianas no son más que dos rectas numéricas que se cortan perpendicularmente. Esto quiere decir que las coordenadas también pueden contener decimales, aunque en esta entrada para no complicar mucho las cosas, nos vamos a quedar con números enteros.

Como hemos dicho, en el sistema de coordenadas cartesianas en dos dimensiones (plano) los ejes (X e Y) se cortan perpendicularmente en el origen (O). Dividen al plano en 4 regiones:

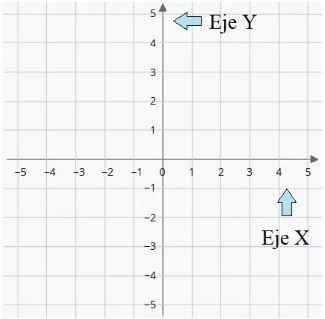
Estas regiones se denominan cuadrantes. Se numeran del 1º al 4º con números romanos en sentido contrario a las agujas del reloj, tomando como punto central el origen.

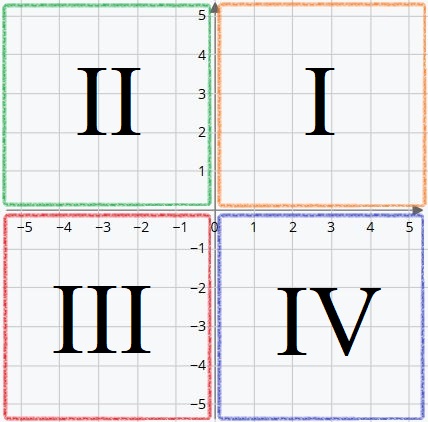
Primer cuadrante

Hasta ahora solo conocíamos el origen ‘O ‘ y el primer cuadrante. En él las coordenadas X e Y siempre son números positivos.

• X positiva significa que la posición está a la derecha del origen.
• Y positiva que está por encima del origen.

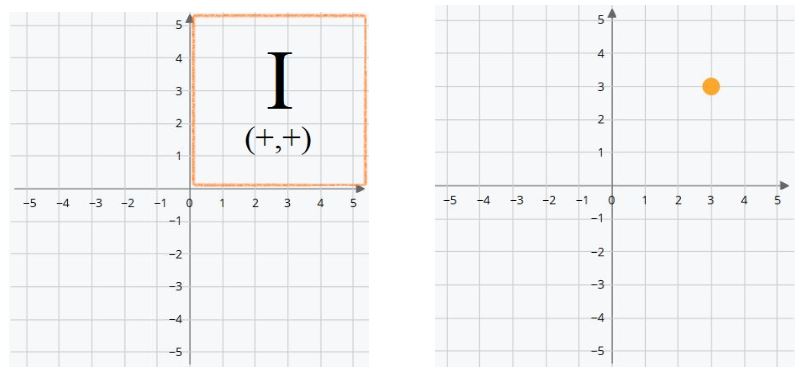
Así que, en este cuadrante, (X,Y) son positivos. Podemos escribirlo de manera abreviada (+,+).

El punto amarillo está en las coordenadas (3,3). Tres posiciones a la derecha del origen y tres hacia arriba.

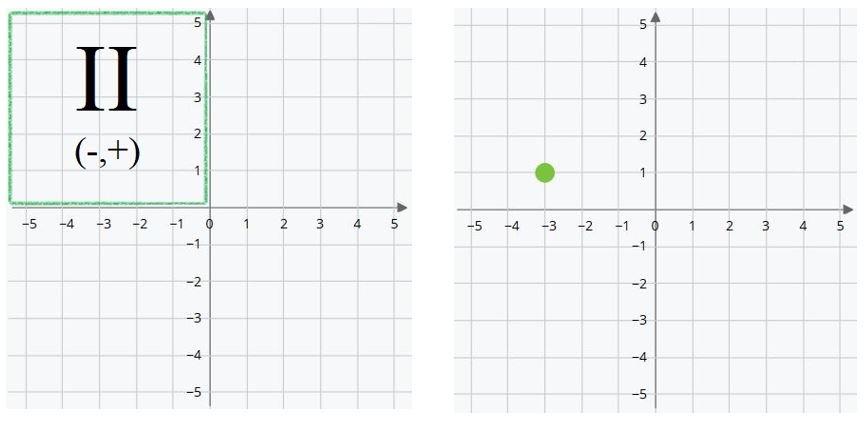
Segundo cuadrante

En este cuadrante aparece la primera coordenada negativa. Los valores positivos nos decían cuántas posiciones contar hacia la derecha o hacia arriba del origen, X e Y respectivamente. De la misma manera los valores negativos indican las posiciones hacia la izquierda o hacia abajo del origen de los ejes X e Y. Por ejemplo, si la coordenada X tiene el valor (-5) significa que está 5 posiciones a la izquierda del origen. Si la Y tiene valor (-1) significa que está una posición por debajo del origen.

• X negativa indica que la posición está a la izquierda del origen.
• Y positiva que está por encima del origen.

De esta manera (X,Y) son (-,+).

En el ejemplo, el punto verde está en las coordenadas (-3,1). Tres posiciones a la izquierda del origen y una posición hacia arriba.

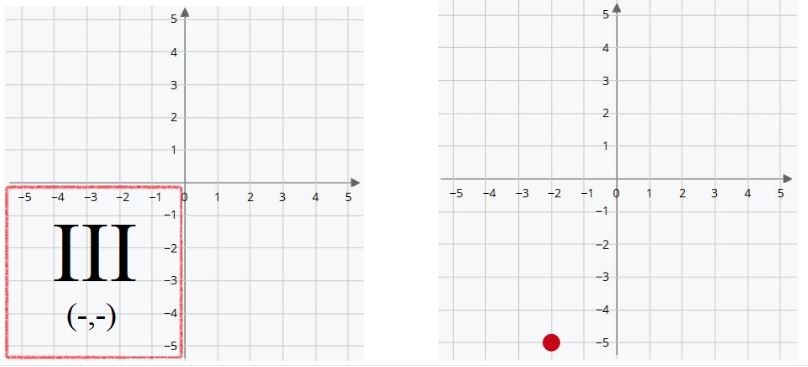
Tercer cuadrante

Aquí ambos valores son negativos.

• X negativa indica que la posición está a la izquierda del origen.
• Y negativa que está por debajo del origen.

Entonces (X,Y) son (-,-).

El punto rojo está en las coordenadas (-2,-5). Dos posiciones a la izquierda del origen y cinco posiciones hacia abajo.

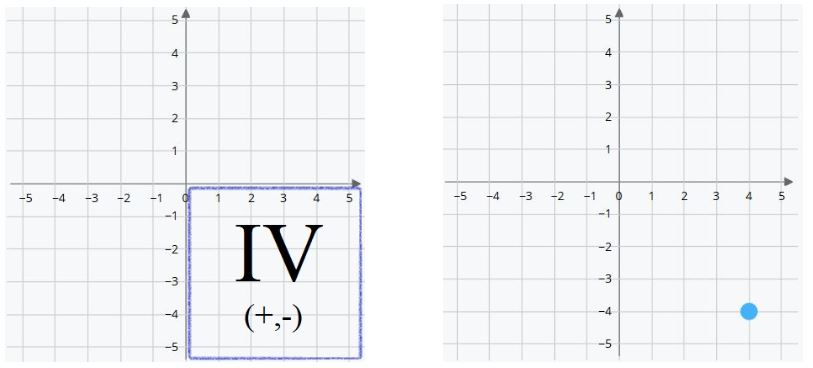
Cuarto cuadrante

El último cuadrante está a la derecha y por debajo del origen. Los valores de X e Y serán positivo y negativo respectivamente.

• X positiva indica que la posición está a la derecha del origen.
• Y negativa que está por debajo del origen.

Por tanto (X,Y) son (+,-).

El punto azul está en las coordenadas (4,-4). Cuatro posiciones a la derecha del origen y cuatro hacia abajo.

En resumen, el valor positivo o negativo de X e Y en las coordenadas indica la posición relativa respecto al origen:

• En el eje X, dirección horizontal, un valor positivo refleja una posición a la derecha del origen. Y uno negativo a la izquierda.
• En el eje Y, dirección vertical, el valor positivo indica una posición por encima del origen. Uno negativo por debajo de él.
• Si X toma el valor cero, la posición de las coordenadas no está ni a la derecha ni a la izquierda del origen. Estaría en algún punto del eje Y.
• Si Y toma el valor cero, la posición de las coordenadas no está ni por encima ni por debajo del origen. Estaría en algún punto del eje X.
• O, el origen, es la única posición en la que ambos valores son cero.

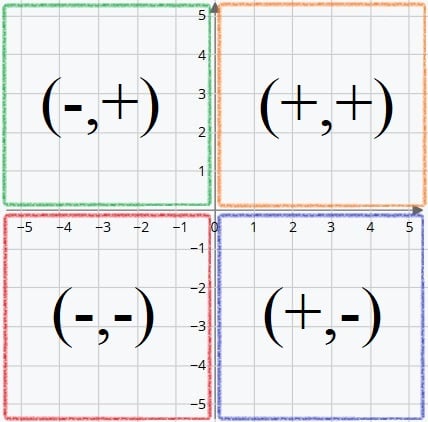
Por tanto, conociendo los valores de (X,Y) podemos saber en qué cuadrante se encuentra esa posición siguiendo el siguiente esquema:

Ejemplos de ejercicios de coordenadas que se hacen en Smartick

Un desplazamiento en coordenadas cartesianas tiene tres elementos:

1. La posición inicial: la coordenada en la que se comienza.
2. El movimiento: los desplazamientos que se realizan.
3. La posición final: la coordenada en la que se acaba tras el movimiento.

Coordenadas iniciales conocidas y movimiento simple con ayuda visual en primer cuadrante

En estos ejercicios se da la posición inicial y el movimiento, que consiste en un solo desplazamiento. Sólo utilizamos el primer cuadrante y preguntamos por la posición final después de realizar el desplazamiento. Además, en los primeros pasos ofrecemos una ayuda visual. Los ejes se diferencian por colores y las coordenadas asignadas a estos ejes mantienen ese código de color. Como estos ejercicios los resuelve alumnado muy pequeño, en lugar de colocar los números sobre las líneas (y a los personajes en las intersecciones de éstas) los colocamos en el centro de la cuadrícula, así resulta más sencillo de ver, pero el resultado es el mismo.

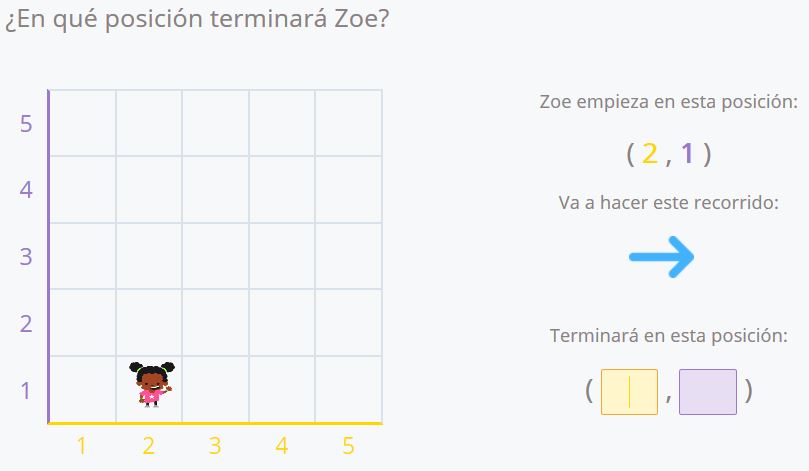
En este ejemplo Zoe comienza en las coordenadas (2,1) y se desplaza una casilla hacia la derecha. Como sólo se desplaza en el eje X, sólo la coordenada X cambia. Su posición final será (3,1).

Coordenadas iniciales conocidas y varios movimientos con ayuda visual en primer cuadrante

Es igual que el anterior con una diferencia: el número de desplazamientos va aumentando.

Max ha comenzado en la posición (4,5). Se ha movido una vez a la izquierda y dos veces hacia abajo. Si seguimos su movimiento a lo largo de la cuadrícula vemos que la posición final es (3,3).

Coordenadas finales conocidas y movimiento con ayuda visual en primer cuadrante

Ahora, en lugar de la posición final, pedimos la posición inicial. Conociendo dónde terminan y los desplazamientos que ha realizado podemos calcularla haciendo el camino inverso.

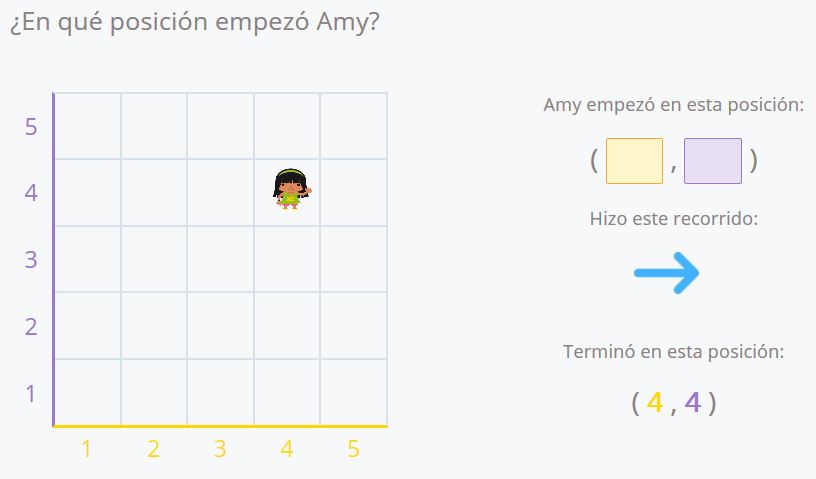
Aquí Amy se ha desplazado una vez a la derecha y ha terminado en la posición (4,4). Siguiendo su desplazamiento hacia atrás (una casilla hacia la izquierda) podemos comprobar que las coordenadas de origen eran (3,4).

La dificultad irá aumentando al incrementarse el número de movimientos.

Ayuda numérica en primer cuadrante

También preguntamos por la posición final o por la inicial, pero ya no se ofrece un apoyo de colores para la identificación de cada coordenada. Además, las coordenadas pasan a ser puntos en el plano en lugar de cuadrados. Si te fijas bien aquí en lugar de estar Eva en el centro de la cuadrícula ya está en la intersección de dos líneas.

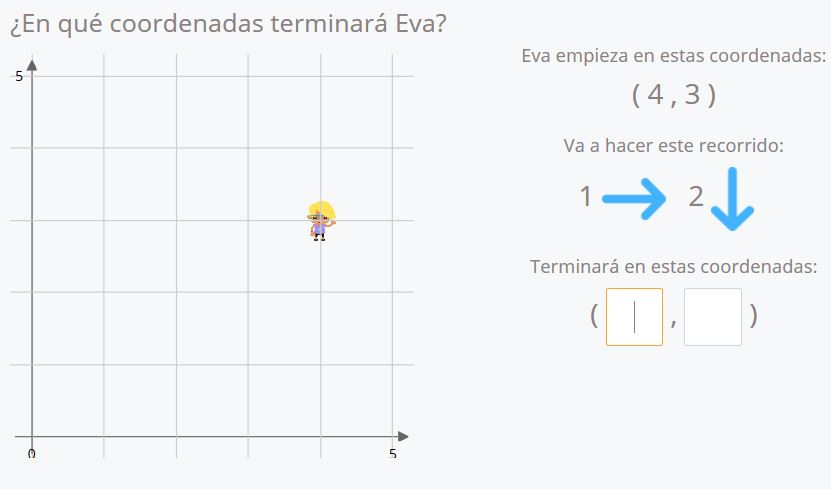
Aquí Eva comienza en la posición (4,3), se mueve una vez a la derecha y dos hacia abajo. Si seguimos los desplazamientos vemos que la posición final de Eva son las coordenadas (5,1).

Todos los cuadrantes

La dinámica es la misma que en las anteriores actividades pero se añaden el resto de cuadrantes.

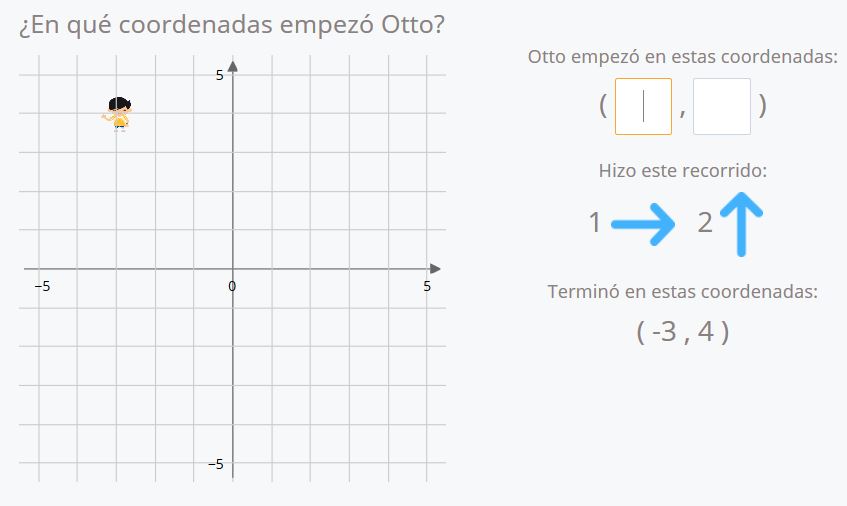Otto se ha desplazado una vez a la derecha y dos hacia arriba. Ha terminado en el punto (-3,4). Si seguimos su recorrido de manera inversa (una vez hacia la izquierda y dos hacia abajo) vemos que las coordenadas de origen son (-4,2).

Y por último aumentamos el tamaño de la cuadrícula por la que se puede mover el avatar.

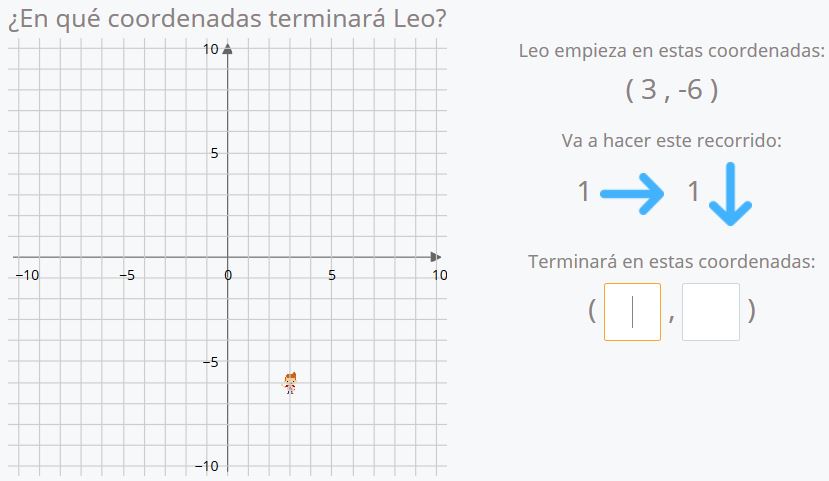
Si Leo comienza en la posición (3,-6) y se desplaza una vez hacia la derecha y una vez hacia abajo… ¿dónde terminará?

¡Eso es! Termina en las coordenadas (4,-7).

Si quieres practicar y conocer más sobre movimiento en coordenadas, y otros contenidos de matemáticas de primaria, personalizados a tu nivel, entra en Smartick y pruébalo gratis.

Para seguir aprendiendo:

• Multiplicar por dos y por tres cifras
• Sumas y restas de números enteros
• Números decimales: Multiplicar y dividir por cifras seguidas de ceros
• Estimaciones de restas con ejemplos y vídeo
• Izquierda y derecha, ¿tan fácil cómo parece?

La diversión es la forma favorita de aprender de nuestro cerebro

Diane Ackerman

Smartick ayuda a tus hijos a aprender de manera divertida

• 15 minutos diarios
• Se adapta al nivel de cada niño
• Millones de estudiantes desde 2009

Prueba GRATIS 7 días

• Acerca de
• Últimas entradas

Alejandro Maculet

Cursando actualmente el Grado de Maestro en Educación Primaria en la Universidad Autónoma de Madrid.
Técnico Superior en Administración y Finanzas, Quiromasajista, Masajista Deportivo y Músico.
Forma parte del equipo de desarrollo de contenidos de Smartick.
Curioso por naturaleza, música y ciencia son dos de sus pasiones.

Últimas entradas de Alejandro Maculet (ver todo)

• Características de la práctica significativa - 23/03/2020
• Cómo representar fracciones en la recta numérica - 10/02/2020
• Diagramas de Venn en Smartick - 13/01/2020