Seguramente ya tengas alguna idea sobre qué es eso que llamamos «ángulo recto». Aún así, te recomiendo que antes de seguir eches un vistazo a otras entradas de nuestro blog que lo explican muy bien. Por ejemplo, puedes repasar esta entrada sobre los diferentes tipos de ángulos.
¿Ya estás preparad@? Pues vamos a ampliar lo que sabes sobre ángulos rectos.
Imagina que…
… te encuentras en la esquina de un campo de fútbol. Ahora, recorres el fondo del campo hasta la otra banda.
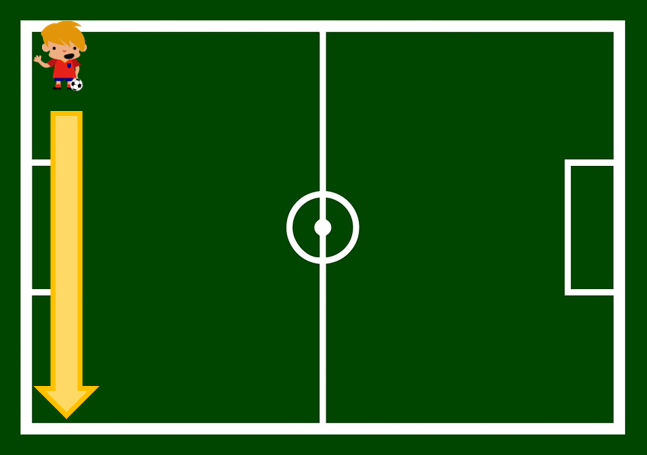
A continuación, giras 90º y vuelves a andar en línea recta hasta el otro fondo.
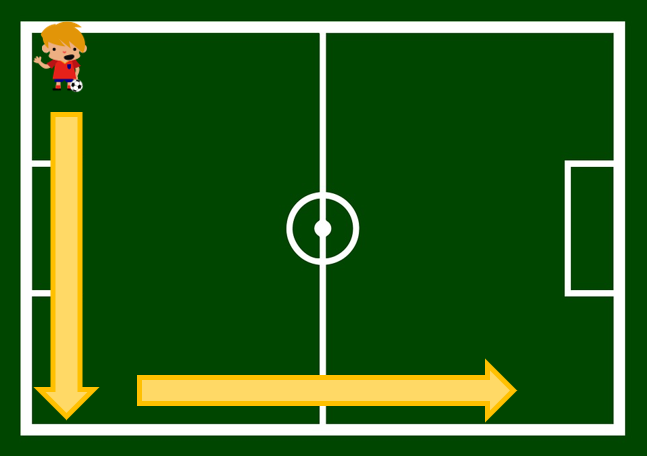
Finalmente, vuelves a girar describiendo un ángulo recto y andas en línea recta de nuevo hasta llegar a la banda.
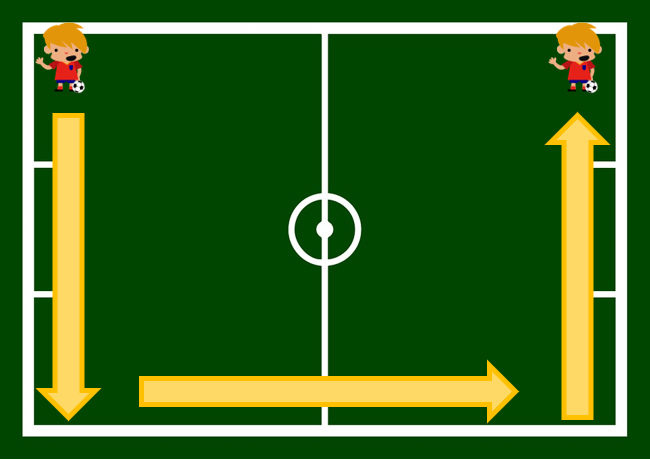
¿Has llegado a un sitio distinto del que estabas originalmente? La respuesta parece obvia, ¿verdad?
Entonces, podríamos aceptar que la secuencia
"Andar recto + Girar 90º + Andar recto + Girar 90º + Andar recto"
nos lleva siempre a un lugar distinto del de partida.
Y si ahora…
fueses un gigante que campa a sus anchas sobre el planeta Tierra y siguieses la secuencia anterior, ¿qué pasaría? ¡Vamos a verlo!
Supongamos que sales del Polo Norte y vas andando recto hacia el sur. Sin embargo, cuando llegas al ecuador, giras formando un ángulo recto y caminas en línea recta sobre él. A continuación, vuelves a girar 90º en el mismo sentido y continúas con tu travesía andando de la misma manera. ¡Mira la imagen siguiente!
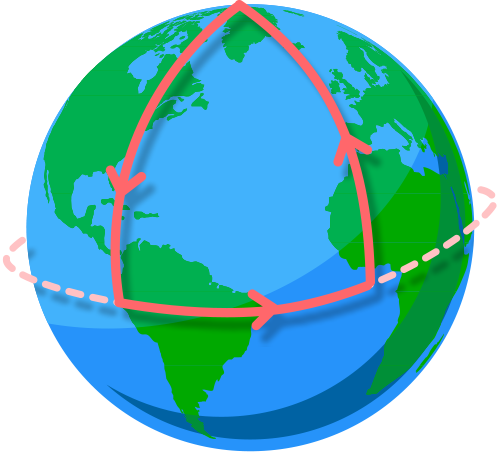
¿Te has dado cuenta de lo que ha ocurrido? En efecto, has regresado al Polo Norte, esto es, al punto de partida. Pero, ¿qué es lo que ha pasado? Podríamos preguntarnos si estos ángulos de 90º que han aparecido sobre la superficie terrestre son también ángulos «rectos». La respuesta es que sí que lo son y, por eso, debemos buscar la explicación en otra parte.
Si te fijas bien, hay una diferencia nada despreciable entre los dos ejemplos. Mientras que en el primer caso, el campo de fútbol era plano, la superficie del segundo es curva. Así, una misma secuencia de movimientos formada solo por «andar en línea recta» y «girar 90º» puede conducir a lugares distintos.
Pero lo interesante es verlo al revés, es decir, que podemos conocer la curvatura de la superficie en la que nos encontramos desde la propia superficie sin tener que viajar hasta la Luna para verlo desde fuera. Este tipo de argumentos son los que utilizan los astrónomos cuando estudian las propiedades del universo.
Espero que este post te haya gustado y te animo a que sigas aprendiendo cosas interesantes de matemáticas con Smartick. ¡Entra y regístrate gratis en nuestro método!
Para seguir aprendiendo:
- Qué es un ángulo obtuso y ejemplos
- Ángulos Complementarios. Qué son y ejemplos
- Ángulo agudo, obtuso, llano y recto
- ¿Qué es un ángulo? ¿Cómo se forma?
- Figuras geométricas: el triángulo
Actualmente está cursando estudios de doctorado en Investigación en educación en la Universidad de Valladolid.
Es profesor de didáctica de la matemática en la Universidad de Valladolid y forma parte del equipo de desarrollo de contenidos de Smartick.
Entre sus aficiones destacan el tenis, el jazz y la escritura.
- Propiedades de las potencias - 13/04/2020
- El porqué de los criterios de divisibilidad - 02/03/2020
- Por qué son importantes los ejemplos en la enseñanza de las matemáticas - 27/01/2020
Que buen servicio.
Muchas gracias Sr Hector