En Smartick apoyamos la combinación de métodos y enfoques pedagógicos para alcanzar la excelencia en el proceso de enseñanza-aprendizaje. Pero esto no surge de un mero capricho, sino que se sustenta en experiencias reales de éxito, que prueban que el mejor camino a seguir en el campo de la educación no es otro que el que bebe de las mejores fuentes, tomando lo mejor de cada método y enfoque.
Holanda, un sistema ejemplar en el uso de algoritmos alternativos
El currículo holandés es un buen ejemplo de la enseñanza de algoritmos alternativos conjuntamente con los tradicionales. Estos son los pasos que deben darse para hacerlo:
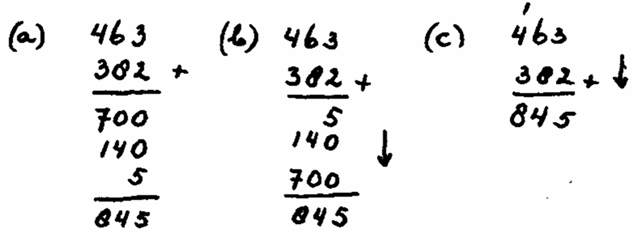
En la imagen, vemos el proceso de aprendizaje del algoritmo tradicional, partiendo del algoritmo alternativo:
a) El algoritmo alternativo implica los siguientes pasos: 400 y 300 son 700; 60 y 80 son 140; y 3 y 2 son 5. Este procedimiento de descomposición se aprende antes en cálculo mental. Después, se suman los resultados parciales mentalmente, mediante un método de encadenado: 700 y 140 son 840; y 5, 845. Como vemos, este algoritmo se desarrolla de izquierda a derecha, que es la forma más “natural” de sumar. Es un algoritmo cerrado basado en números, pues no se suman 4 y 3 en las centenas, sino 400 y 300.
b) Se muestra un algoritmo «de transición». No es un algoritmo pensado para realizarse habitualmente, sino para servir de “puente” entre el algoritmo alternativo y el tradicional. Su única diferencia con el alternativo, es que la operación procede de derecha a izquierda, que es algo que no debe generar problemas, pues da igual comenzar por un lado o por otro la operación cuando no hay “llevada”.
c) Vemos el algoritmo tradicional, que es una forma comprimida del «de transición» en la que escribimos las sumas parciales en una única línea.
Las claves didácticas
Las claves didácticas de esta secuencia de paso del algoritmo alternativo al tradicional son las siguientes:
- Los algoritmos en Holanda se estudian más tarde, y se les dedica mucho menos tiempo. Previamente, los alumnos han estudiado cálculo mental, y los algoritmos se apoyan en los métodos de cálculo mental de descomposición y encadenado.
- El algoritmo alternativo se aprende primero, porque es el más natural, es más sencillo de comprender. Favorece también la comprensión del valor posicional, integra el cálculo escrito con el cálculo mental y con la estimación, y evita la dificultad de falta de comprensión de la llevada en la suma. Desde el punto de vista didáctico, posee grandes ventajas con respecto al algoritmo tradicional.
- El paso del algoritmo alternativo al tradicional no es inmediato y requiere un trabajo didáctico específico, que da lugar a un algoritmo de transición. Tiene características del algoritmo alternativo y otras del tradicional (paso b en la imagen anterior). Está, por así decirlo, en el punto medio entre los dos algoritmos, y sirve de “puente” entre ellos.
- Después se estudia el algoritmo tradicional. Pero el estudio previo del algoritmo alternativo ayuda a comprender el algoritmo tradicional, que es “menos didáctico”.
- Al final, los estudiantes conocen dos algoritmos, el alternativo y el tradicional. Cada algoritmo facilita la comprensión de aspectos distintos del sistema de numeración decimal. Con el alternativo, se aprende mejor el valor posicional de los números. Con el tradicional se acaba también comprendiendo la llevada.
Por eso, en Smartick optamos por una enseñanza de los algoritmos de la suma y la resta que combina el uso del algoritmo tradicional con los algoritmos alternativos como herramienta de apoyo para la comprensión del mismo. Si quieres descubrir como lo hacemos, no dudes en registrarte en Smartick y probarlo gratis.
Para seguir aprendiendo:
- ¿Es bueno utilizar algoritmos alternativos como ABN “mezclados” con los tradicionales?
- Resta con llevada: explicación con dos algoritmos diferentes
- Algoritmo de la suma. Suma en vertical con llevadas
- Algoritmos Abiertos Basados en Números: El método ABN
- El valor posicional de los números








Considero que debemos permitir al estudiante explorar otras formas de resolución ; las heruristica para la resolución de un problema plantea el desarrollo de estrategías descriptivas, nunca prescriptivas que le puedan ayudar al estudiante a encontrar diferentes manera para llegar a su meta en la solución de un problema.