Desde el blog de Smartick continuamos reflexionando al hilo de la lectura del libro de Craig Barton Cómo me gustaría haber enseñado matemáticas. Hoy abordamos el tema del uso de preguntas diagnósticas en la Educación Matemática.
Enseñanza diagnóstica
La enseñanza diagnóstica tiene una larga tradición dentro de la Educación Matemática. Este enfoque de la enseñanza de las matemáticas se desarrolló inicialmente, en los años 80, en el Shell Centre de la Universidad de Nottingham. Fue impulsada por investigadores como Hugh Burkhardt y Malcolm Swan. La Comisión Internacional para la Enseñanza de las Matemáticas (ICMI) reconoció este trabajo en 2016 concediendo a ambos el primer Premio Emma Castelnuovo a la excelencia en la práctica de la Educación Matemática.
La enseñanza diagnóstica es una forma de evaluación formativa para el aprendizaje que aúna la investigación con el desarrollo curricular en matemáticas. En ella tienen una importancia decisiva las preguntas diagnósticas.
Preguntas diagnósticas
Las preguntas diagnósticas son cuestiones cerradas, de elección múltiple, que permiten identificar y comprender con precisión y eficiencia los fallos y las ideas equivocadas de los alumnos en su aprendizaje de las matemáticas. Ayudan al profesorado a detectar, de forma rápida, cómo está el nivel de la clase en aspectos cruciales para poder enfocar la enseñanza de un tema. Constituyen un método de diagnóstico inicial, y están diseñadas partiendo del conocimiento que tenemos de resultados de investigación sobre las dificultades de aprendizaje matemático de los alumnos.
Fallos y errores en matemáticas
Uno de los objetivos del uso de preguntas diagnósticas es diferenciar cuando un alumno tiene un fallo y cuando comete un error que refleja una idea equivocada. Los fallos en matemáticas no son verdaderamente errores. Suelen deberse a una falta de atención, pero no son sistemáticos. Un alumno puede despistarse y decir que 7 y 6 son 12, tras contar con los dedos a partir del 7. Seguramente, la siguiente vez que haga una suma igual, la hará bien y no requerirá una intervención o ayuda especial para corregir esta “errata”. Sin embargo, los errores reflejan un patrón, son resultado de un conocimiento deficiente o incompleto. Los errores suelen ser persistentes e, incluso después de intentar corregirlos explícitamente, vuelven a aparecer.
Errores en el uso del signo igual
Sabemos que el uso del signo igual provoca dificultades y errores persistentes. Uno de ellos se produce cuando concatenamos dos operaciones aritméticas. Al pedir a los alumnos que calculen mentalmente 8 + 5, muchos responden “Ocho y dos diez, y tres, trece”. Si, a continuación, solicitamos que anoten este cálculo en su cuaderno, bastantes lo escribirán como 8 + 2 = 10 + 3 = 13. Lo correcto, en este caso, sería separar las dos igualdades así: 8 + 2 = 10; 10 + 3 = 13. Ese tipo de error es muy frecuente, primero en la aritmética de Educación Primaria, y después en el álgebra de la Educación Secundaria. La igualdad 8 + 2 = 10 + 3 no es correcta, porque la parte izquierda suma 10 y la parte de la derecha, 13. No pueden unirse, por tanto, ambas expresiones con un signo igual.
Ejemplos de preguntas diagnósticas en Smartick
Smartick propone tareas a los alumnos, al inicio de su trabajo en álgebra, que siguen el enfoque de las preguntas diagnósticas. La siguiente, trata de valorar si se comprende que dos productos, con dos factores distintos de cero, si coincide uno de los factores en ambos productos, sólo pueden ser iguales si coincide el otro factor. En este caso, además, estamos ante un caso particular de la propiedad conmutativa del producto. Así, solo la primera opción entre las siguientes representa una igualdad correcta. Lo mismo ocurriría con la suma: a + b = c + b. Solo puede ser una igualdad correcta en caso de que a = c.
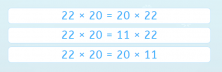
Presentamos, a continuación, otro ejemplo de pregunta diagnóstica en la que hay que seleccionar las opciones correctas. Con preguntas como esta, podemos valorar rápidamente si los alumnos conocen la propiedad conmutativa de la suma (opción B) y se dan cuenta, además, de que esta propiedad no se puede generalizar a la resta (opción C).
Cómo ayudan las preguntas diagnósticas en la planificación de la enseñanza de temas nuevos
¿En qué situación se convierten tareas de este tipo en preguntas diagnósticas? Cuando vamos a comenzar a resolver ecuaciones de primer grado e interesa diferenciar casos en que las ecuaciones tengan una solución, infinitas, o ninguna. El conocimiento que evaluamos sobre el signo igual, en preguntas diagnósticas como las anteriores, es el que permite distinguir entre estos casos sin necesidad de realizar operaciones. Así, en el caso (1), la ecuación no puede tener solución, dado que 3 no es igual a 2; en la ecuación (2) tenemos una única solución (x=0); y la ecuación en (3) tiene infinitas soluciones, pues se cumple para cualquier valor de x. Este pequeño diagnóstico es el que me permite decidir si los alumnos tienen los conocimientos previos necesarios sobre el signo igual. De lo contrario, me convendrá hacer un repaso, para poder abordar la iniciación a las ecuaciones con mayor garantía de éxito.
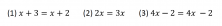
Dentro de las sesiones diarias de matemáticas en Smartick hay diversas preguntas diagnósticas propuestas para valorar el nivel de competencia matemática de cada alumno. Esto nos permite ofrecerles el mejor camino para hacer un aprendizaje personalizado de las matemáticas, que tenga en cuenta las posibles debilidades y fortalezas de su pensamiento matemático.
Para seguir aprendiendo:
- El signo en la potencia
- Sumas y restas de números enteros
- El debate sobre Educación en España en los medios
- Smartick para la enseñanza-aprendizaje de las matemáticas
- Ortografía natural, arbitraria y reglada con ejemplos
Fundador de la revista Edma 0-6: Educación Matemática en la Infancia. Miembro de la SEIEM.
Entusiasmado por la Educación Matemática en los primeros años. Cambiar la Educación Matemática es posible.
Buena la enseñanza, me gustó mucho.