Hace unos meses hablábamos en este post sobre las diferencias entre el ábaco holandés rekenrek frente al tradicional japonés sorobán y la analogía con las manos. Hoy comentaremos las ventajas del rekenrek frente al sorobán para favorecer estrategias variadas en los niños al hacer un mismo cálculo.
Una de las diferencias entre el uso del sorobán y del rekenrek es que al utilizar el sorobán cada operación se puede hacer de una única forma, mientras que con el rekenrek favorecemos que los estudiantes puedan emplear varias estrategias para un mismo cálculo. Para explicar esto, comenzamos explicando cómo se suma en el sorobán. Supongamos que queremos sumar 6. En el sorobán hay tres formas diferentes de sumar el 6 dependiendo de a qué número le sumemos el 6. Para ilustrar las tres formas, vamos a ir sumando de 6 en 6.
Partimos de la posición 0 en el sorobán, en que todas las cuentas están alejadas de la barra horizontal que separa las cuentas de arriba, que valen 5, de las cuentas de abajo, que valen 1. Operamos en la primera varilla de la derecha, la de las unidades (la segunda es la de las decenas, etc.). Para sumar 6, tenemos que acercar a la barra horizontal una cuenta superior y una inferior. Sumar 6 es sumar 5 y 1 (6 = 5 + 1).
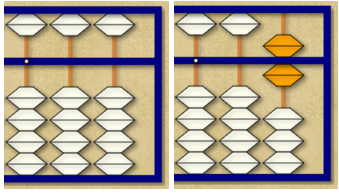 Si queremos sumar otros 6, ya no podemos sumar 5 y 1, puesto que la cuenta del 5 está ya puesta. Podemos pensar que el 6 = 10 – 4. Poner 10 es añadir una cuenta en la siguiente varilla (de las decenas), pero para quitar 4, dado que no hay 4 cuentas, debemos quitar 5 y poner 1. En realidad, para sumar 6 estamos haciendo 6 = 10 – 5 + 1, lo que en el ábaco significa añadir una cuenta de abajo en la segunda varilla, quitar la cuenta superior de la primera varilla y añadir una cuenta inferior en la primera varilla.
Si queremos sumar otros 6, ya no podemos sumar 5 y 1, puesto que la cuenta del 5 está ya puesta. Podemos pensar que el 6 = 10 – 4. Poner 10 es añadir una cuenta en la siguiente varilla (de las decenas), pero para quitar 4, dado que no hay 4 cuentas, debemos quitar 5 y poner 1. En realidad, para sumar 6 estamos haciendo 6 = 10 – 5 + 1, lo que en el ábaco significa añadir una cuenta de abajo en la segunda varilla, quitar la cuenta superior de la primera varilla y añadir una cuenta inferior en la primera varilla.
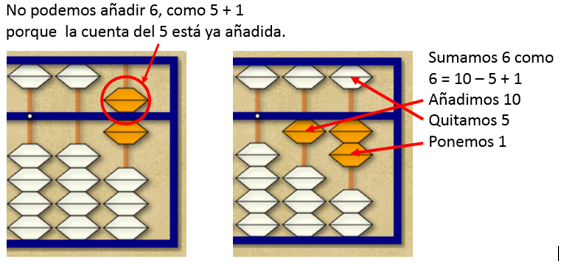
Para sumar 6 más, no hay problema, puesto que volvemos a tener disponibles las cuentas de 5 y de 1. El resultado (de 12 + 6) es 18.
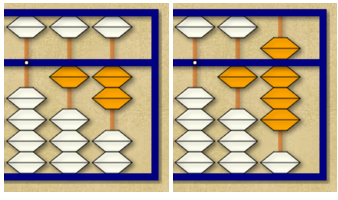
Para sumar 6 más, debemos hacerlo como en el segundo paso (6 = 10 – 5 + 1).
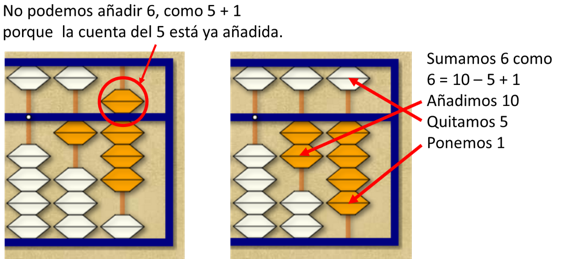
Por último, hay una tercera forma de sumar 6, que se da en esta situación, que es (6 = 10 – 4), y que consiste en añadir 1 decena y quitar 4 cuentas de valor 1.
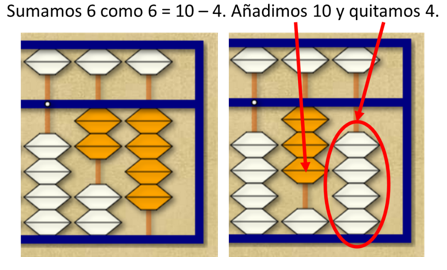 Resumiendo, cada suma se puede hacer de tres formas diferentes, dependiendo de la disponibilidad de cuentas del ábaco. El 6 puede sumarse como 5 + 1, 10 – 4, o 10 – 5 + 1, pero siempre que hacemos un cálculo concreto (4 + 6) lo hacemos igual (4 + 6 = 4 + 10 – 4), añadiendo una cuenta de 10 y quitando 4 cuentas de 1. Se trata, por tanto de un proceso totalmente algorítmico que no admite variaciones. No hay distintas estrategias para hacer una suma. Sin embargo, en el rekenrek, como vamos a ver en el ejemplo siguiente, se pueden utilizar diferentes estrategias para un mismo cálculo. Por ejemplo, para hacer 7 + 5, se puede poner el 7 en la fila superior y el 5 en la inferior, y contar a partir del 7 hasta llegar a la solución. Este es un método de conteo a partir de un número que es muy importante adquirir en primer curso de educación primaria.
Resumiendo, cada suma se puede hacer de tres formas diferentes, dependiendo de la disponibilidad de cuentas del ábaco. El 6 puede sumarse como 5 + 1, 10 – 4, o 10 – 5 + 1, pero siempre que hacemos un cálculo concreto (4 + 6) lo hacemos igual (4 + 6 = 4 + 10 – 4), añadiendo una cuenta de 10 y quitando 4 cuentas de 1. Se trata, por tanto de un proceso totalmente algorítmico que no admite variaciones. No hay distintas estrategias para hacer una suma. Sin embargo, en el rekenrek, como vamos a ver en el ejemplo siguiente, se pueden utilizar diferentes estrategias para un mismo cálculo. Por ejemplo, para hacer 7 + 5, se puede poner el 7 en la fila superior y el 5 en la inferior, y contar a partir del 7 hasta llegar a la solución. Este es un método de conteo a partir de un número que es muy importante adquirir en primer curso de educación primaria.
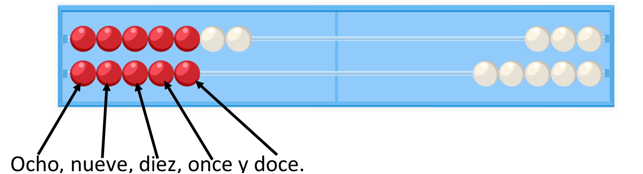
También se puede reconocer inmediatamente (subitización) que las cinco rojas de arriba y las de abajo son 10 y que, con las 2 blancas, el resultado es 12. Esto es, 7 + 5 = 5 + 5 + 2 = 10 + 2 = 12. Esta estrategia se conoce como “uso de dobles más dos”.

Podemos quitar una cuenta de arriba y pasarla abajo, física o mentalmente, para reconocer que 7 + 5 = 6 + 6 = 12, reduciendo de nuevo el cálculo a un uso de dobles.

También podemos añadir dos cuentas blancas abajo, reconocer que estamos haciendo un doble, y luego compensar quitando los dos que hemos añadido. 7 + 5 = 7 + 7 – 2. A esta estrategia se le llama “uso de dobles menos 2”.

Por último, podemos añadir las cuentas que faltan para el 10, descomponiendo el 5 en 3 (lo que falta al 7 para llegar a 10) y 2 (lo que queda por sumar). A esta estrategia la llamamos “paso al 10” y se podría representar como 7 + 5 = 7 + (3 + 2) = (7 + 3) + 2 = 10 + 2 = 12.
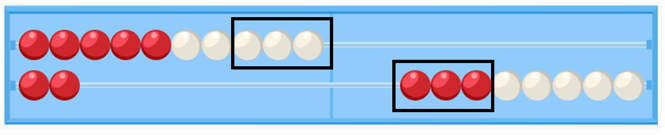 Resumiendo, con el rekenrek podemos hacer la misma operación (7 + 5) de 5 formas diferentes. Pensamos que tiene un gran valor que los niños aprendan a calcular con flexibilidad, que conozcan varias estrategias para un mismo cálculo y que elijan la estrategia que les parezca más adecuada en cada caso. Cuando hablamos de cálculo mental, no solo nos referimos a calculo hecho “de cabeza”, o sin ayudas externas, sino que hablamos de un cálculo flexible, que potencie el desarrollo del sentido numérico, y no de un cálculo rígido y algorítmico, que puede desarrollarse de forma mecánica. Por eso en Smartick hemos introducido desde hace unos meses el rekenrek en las sesiones de los más pequeños.
Resumiendo, con el rekenrek podemos hacer la misma operación (7 + 5) de 5 formas diferentes. Pensamos que tiene un gran valor que los niños aprendan a calcular con flexibilidad, que conozcan varias estrategias para un mismo cálculo y que elijan la estrategia que les parezca más adecuada en cada caso. Cuando hablamos de cálculo mental, no solo nos referimos a calculo hecho “de cabeza”, o sin ayudas externas, sino que hablamos de un cálculo flexible, que potencie el desarrollo del sentido numérico, y no de un cálculo rígido y algorítmico, que puede desarrollarse de forma mecánica. Por eso en Smartick hemos introducido desde hace unos meses el rekenrek en las sesiones de los más pequeños.
Para seguir aprendiendo:
- Aprende a sumar con la ayuda del Rekenrek
- Rekenrek versus Sorobán I: La analogía con las manos
- Estrategias de cálculo mental para niños
- Sumas y restas en horizontal. Cálculo mental
- Sumas y restas incompletas para desarrollar la flexibilidad matemática








Hola, me gustaría que por favor me proporcionaran información sobre costos de inscripción
Hola Pilar:
El coste de Smartick depende del número de niños que suscribas y la duración del compromiso de permanencia.
No sé desde qué país nos haces la consulta. Por favor, escribe un correo a mis compañeras de atención al cliente: [email protected] y ellas podrán ayudarte.
Un saludo!