En el post de hoy vamos a aprender cómo aplicar las barras de Singapur en problemas con fracciones. Si no sabes lo que es una barra de Singapur, puedes ver nuestro post de suma y resta con las barras de Singapur o el de multiplicación y división con las barras de Singapur.
Vamos a ver unos cuantos ejemplos para que nos quede clarísimo. Eso sí, los números los hemos puesto fáciles porque lo importante en este post nos es la cuenta sino cómo se usan las barras para hacer fracciones.
Primer problema de fracciones resuelto con la ayuda de barras de Singapur

En una granja hay 24 animales. Dos tercios de ellos son vacas. ¿Cuántas vacas hay?
Ponemos todos los datos en nuestra barra:
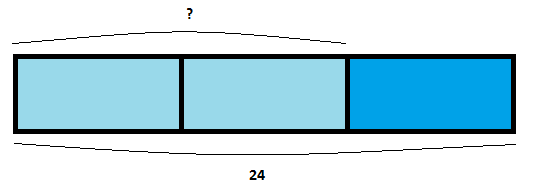
Entonces, como vemos tenemos que tres unidades son 24 animales, primero podemos calcular cuánto es una unidad para luego multiplicar para hallar cuántos animales son dos unidades. Es decir:
- 3 unidades = 24
- 1 unidad = 24 : 3 = 8
- 2 unidades = 2 x 8 = 16
En la granja hay 16 vacas.
Segundo problema de fracciones
Ahora tenemos un granja con 36 animales, en la que dos tercios son vacas. ¿Cuántos animales no son vacas?
Dibujamos nuestra barra de Singapur con los datos:
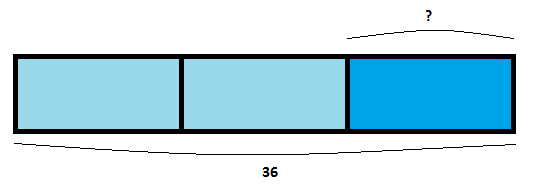
¡Es muy parecido al problema anterior! La diferencia es que aquí la parte que nos interesa es otra, un tercio. Entonces solo tenemos que encontrar cuánto vale la unidad, es decir, dividir entre 3.
- 3 unidades = 36
- 1 unidad = 36 : 3 = 12
Así que en la granja hay 12 animales que no son vacas.
Tercer problema de fracciones

He preparado un ramo de flores para regalar a mi madre. Dos tercios del ramo son violetas y el resto son margaritas. Si el ramo tiene 16 violetas, ¿cuántas flores tiene el ramo?
En la barra de Singapur lo ponemos así:
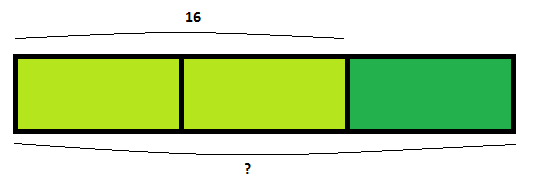
La clave es hacer lo mismo que en los anteriores problemas, primero calculamos cuánto es una de las partes y luego buscamos cuánto es la parte que queremos, en este caso las tres partes:
- 2 unidades = 16
- 1 unidad = 16 : 2 = 8
- 3 unidades = 3 x 8 = 24
El ramo tiene 24 flores.
Cuarto problema de fracciones
Mi hermana me quiere copiar el regalo, así que también le ha comprado un ramo de margaritas y violetas. Si dos tercios de su ramo son margaritas y tiene 20 margaritas, ¿cuántas violetas tiene?
Dibujamos la barra:
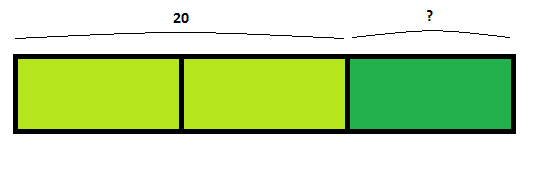
Es fácil ver que las margaritas representan dos unidades. Entonces, ¿cuánto son 3 unidades? Hallamos cuánto es una y luego multiplicamos por 3:
- 2 unidades = 20
- 1 unidad = 20 : 2 = 10
El ramo tenía 10 violetas.
Quinto problema de fracciones

En mi campamento hay un montón de niños. Sé que hay 75 chicas y también sé que hay tres quintas partes de chicos que de chicas. ¿Cuántos niños hay en el campamento?
Este caso es diferente a los anteriores porque vamos a necesitar dos barras de Singapur:
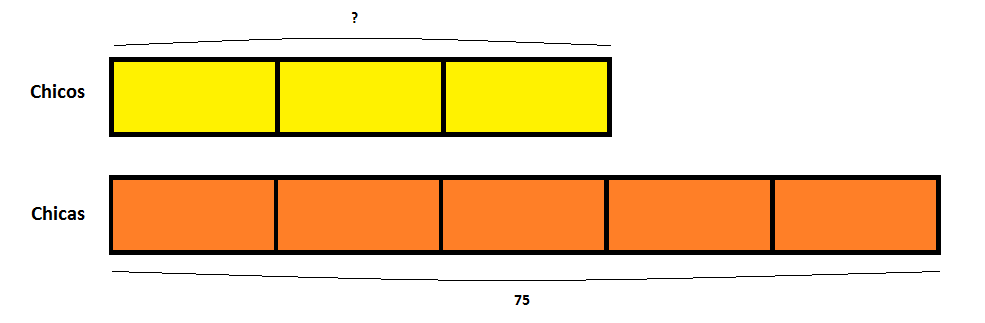
Como sabemos cuánto valen 5 partes, podemos reducirlas a una y luego ver cuánto valen 3 partes:
- 5 unidades = 75
- 1 unidad = 75 : 5 = 15
- 3 unidades = 15 x 3 = 45
Es decir, hay 45 niños en el campamento.
Sexto problema de fracciones
Si nos piden la otra cantidad también es muy fácil de hacer:
En mi campamento hay 15 niños, lo que supone tres quintas partes de chicos que de chicas. ¿Cuántas chicas hay en el campamento?
Dibujamos las dos barras:
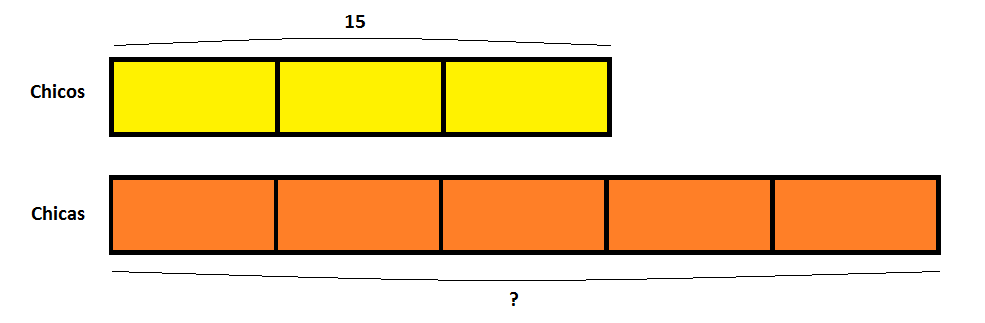
Este caso es muy parecido al anterior. Tenemos que ver cuánto es una parte y luego hallar las cinco partes.
- 3 unidades = 15
- 1 unidad = 15 : 3 = 5
- 5 unidades = 5 x 5 = 25
Así que hay 25 niñas en el campamento.
Séptimo problema de fracciones

Mi padre ha comprado para mi fiesta de cumpleaños naranjas y fresas para hacer batidos. Ha comprado 50 fresas y de naranjas tres quintos de la cantidad de las fresas. ¿Cuántas frutas ha comprado en total?
Otra vez, nos hacen falta dos barras: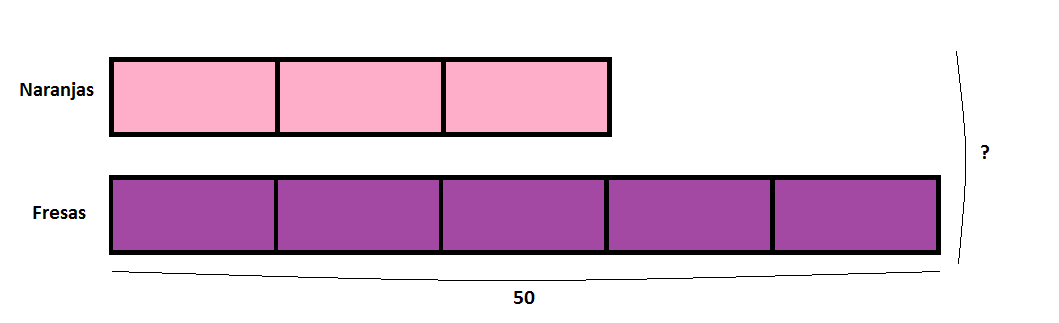 Como en los casos anteriores, reducimos a la unidad para ver cuánto vale una y luego multiplicamos, pero esta vez por todas las unidades, es decir, 5 + 3 = 8.
Como en los casos anteriores, reducimos a la unidad para ver cuánto vale una y luego multiplicamos, pero esta vez por todas las unidades, es decir, 5 + 3 = 8.
- 5 unidades = 50
- 1 unidad = 50 : 5 = 10
- 8 unidades = 10 x 8 = 80
Ha comprado 80 frutas en total.
Octavo problema de fracciones
Como vienen más amigos a la fiesta, mi madre ha vuelto a ir a comprar y ha traído 45 naranjas, otra vez, tres quintos de la cantidad de fresas que ha comprado. ¿Cuánta fruta ha traído esta vez?
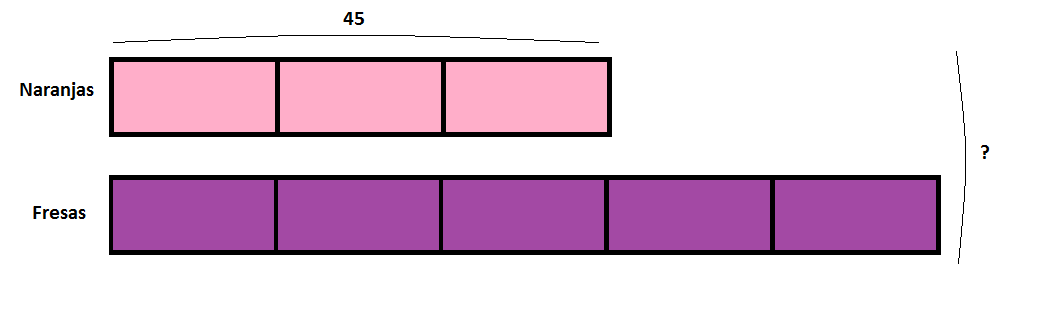
Igual que antes, sabemos cuánto son tres partes: 45 naranjas. Así que reducimos a una unidad y luego multiplicamos por todas las unidades.
- 3 unidades = 45
- 1 unidad = 45 : 3 = 15
- 8 unidades = 15 x 8 = 120
Entonces mi madre ha comprado 120 frutas en total, 45 naranjas y 75 fresas.
¡Ya está! ¿Se te ocurren más ejemplos de barras de singapur aplicadas a las fracciones?
En Smartick utilizamos este recurso para que te sientas más cómodo y aprendas mucho más rápido, así que apúntate para retarte a ti mismo y probar cuánto has aprendido hoy.
Y si quieres aprende más matemáticas de primaria, adaptadas a tu nivel, entra en Smartick, regístrate y pruébalo gratis.
Para seguir aprendiendo:
- Barras de Singapur aplicadas al concepto de porcentaje
- Barras de Singapur aplicadas a la resolución de ecuaciones algebraicas I
- Barras de Singapur aplicadas a la suma de fracciones
- Barras de Singapur aplicadas a la resolución de problemas II
- ¿Qué es un ratio? Lo aprendemos con la ayuda de las Barras de Singapur
- Figuras geométricas. Clasificación, tipos y ejemplos - 20/03/2017
- Nuevos contenidos de Smartick - 11/07/2016
- Ejercicios de lógica en Smartick II - 23/06/2016








Gracias!
Felicitaciones!!!! las explicaciones están en forma muy clara la solución de los problemas por el método de barra.
Excelente, me encantó la explicación y la aplicación del método de barra, para el planteamiento y solución de los diversos problemas. Felicitaciones