¿Sabes qué es un cilindro? En este post te lo explicamos. Además, veremos cuál es su desarrollo, las partes que lo componen y aprenderás a calcular su área y si volumen. También te presentamos algunas de las actividades sobre identificación de cilindros que hacen los alumnos en Smartick, el método online de aprendizaje de matemáticas de primaria.
Índice
¿Qué es un cilindro?
Un cilindro es un cuerpo geométrico que está formado por un rectángulo que gira alrededor de uno de sus lados. En matemáticas, también se define como la superficie cilíndrica que se forma cuando una recta llamada generatriz gira alrededor de otra recta paralela, a la que llamamos eje.
Para aclarar este concepto, debemos tener en cuenta si estamos hablando de un cilindro sólido, es decir, de un cuerpo geométrico. O de la superficie del cilindro a la que llamamos cilindro hueco. Lo vemos a continuación con un ejemplo:

Los cálculos que vamos a hacer en esta entrada son para cilindros sólidos.
Tipos de cilindros
Hay dos tipos de cilindro:
Cilindro rectangular
Cuando el eje del cilindro es perpendicular a las bases.
Cilindro oblicuo
Si el eje no es perpendicular a las bases.

¿Cómo es el desarrollo de los cilindros?
El desarrollo de un cuerpo geométrico es ver en un plano toda la superficie del mismo, en este caso, la superficie de un cilindro sólido. Pero, ¡cuidado!, tiene que ser con tapas, es decir, con las bases, porque si «desarrollas» por ejemplo, el rollo del papel higiénico, solo tendrías un rectángulo.
El desarrollo de un cilindro consta de un rectángulo, que es la parte lateral del cilindro y de dos círculos, que son las dos bases del mismo. Si quieres puedes entrar en el post de figuras geométricas para recordar las principales características de los rectángulos o de los círculos.

¿Qué elementos tienen los cilindros?
Cuando generamos un cilindro girando un rectángulo:
- El eje es el lado del rectángulo que permanece fijo en el giro.
- Las bases son dos círculos, perpendiculares al eje. Son las tapas que cierran el cilindro.
- La altura es la distancia entre las dos bases.
- El radio (r) es la longitud desde el eje hasta el extremo del cilindro. Corresponde con el radio de la base.
¿Cómo se calcula el área de un cilindro?
Hay que considerar el desarrollo del cilindro y calcular el área de sus partes, esto es, la del rectángulo y la de las dos bases.

Área del rectángulo = 2 × π × r × h
Área de la base = π × r2 (¡Recuerda que tiene dos bases!)
Sumando todo obtenemos el área = 2 × π × r × h + 2 × π × r2
Área = 2 × π × r × ( h + r )
Ejemplo de área de cilindro
- Calcular el área de un cilindro de radio 3 cm y de altura 60 mm.
En primer lugar, debemos poner tanto el radio como la altura en las mismas unidades. Por eso tenemos que pasar la altura de milímetros a centímetros. Si quieres puedes ver nuestro post sobre problemas de conversión de medidas de longitud que te ayudará a refrescar la memoria para realizar el cambio de unidades.
60mm = 6cm
Ahora, vamos a calcular el área del rectángulo que equivale a la superficie lateral del cilindro. Como ya habíamos indicado antes su fómula, lo sustitumos por los valores del cilindro:
Área del rectángulo = 2 × π × r × h
2 × 3,14 × 3 × 6 = 113,04 cm²
A continuación, tenemos que calcular el área de las bases, que es igual al área de una base pero por 2. Cogemos la fórmula que ya habíamos indicado al principio y también sustituimos los valores:
Área de la bases = 2 × π × r2
2 × 3,14 × 9 = 56,52 cm²
Y para terminar, sumamos las partes del cilindro, es decir, el área lateral que es el área del rectángulo y el área de las bases:
Área del cilindro = 2 × π × r × h + 2 × π × r2
113,04 + 56,52 = 169,56 cm²
¿Cómo se calcula el volumen del cilindro?
El volumen es igual al área de la base por la altura, recuerda que solemos indicar la altura con la letra «h».
Volumen = π × r2 × h
Ejemplo de volumen de cilindro
- Calcular el volumen de un cilindro de radio 5 cm y de altura 60 mm.
Como hemos indicado antes, debemos poner tanto el radio como la altura en las mismas unidades. Pasamos la altura de milímetros a centímetros:
60mm = 6cm
Para calcular el área de la base multiplicamos por π el radio al cuadrado:
Área de la base = π × r2
3,14 × 25 = 78,50 cm²
Y para hallar el volumen del cilindro tenemos que multiplicar el área de la base por 6 cm que es lo que mide la altura:
78,50 × 6 = 471 cm³
Para calcular este volumen hemos multiplicado un área (unidades cuadradas) por una altura (unidades lineales), por eso nos han salido unidades cúbicas. Recuerda que la unidad de medida del volumen en el Sistema Internacional de Unidades es el metro cúbico (m³), aunque nosotros hemos usado cm³, que es un submúltiplo suyo.
Lo que hemos calculado vale tanto si el cilindro es recto como si es un cilindro oblicuo. Piénsalo, es como si la torre de monedas con la que representábamos un cilindro oblicuo la pusierámos recta, ambas tendrían el mismo volumen.
Ejemplos de ejercicios de identificación de figuras geométricas en Smartick
A continuación, vamos a ver los distintos tipos de ejercicios que tenemos en Smartick para aprender a identificar un cilindro.
Identificar figuras geométricas
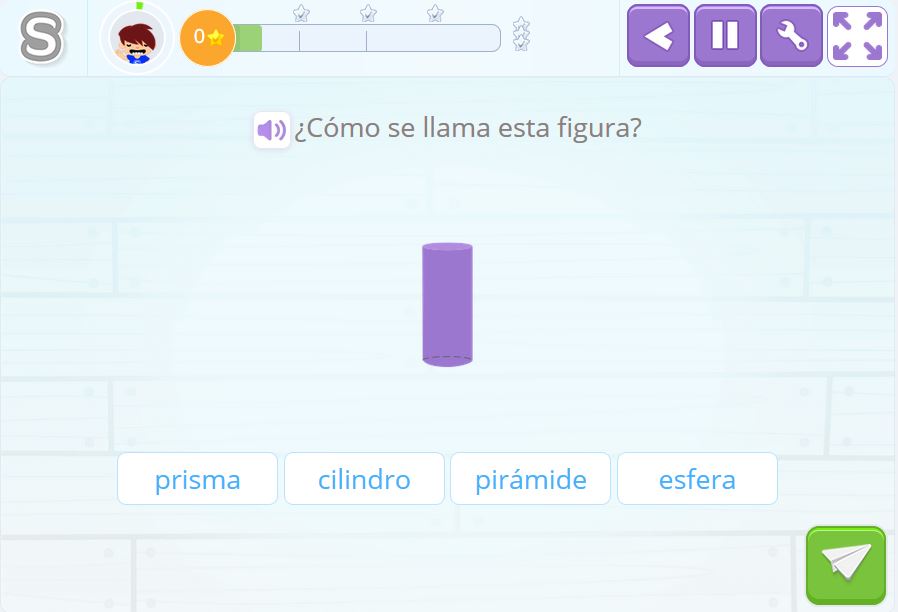
Identificar el cuerpo geométrico de la imagen
Aparece un cuerpo geométrico, el alumno debe identificarlo y marcar su nombre de entre las diversas opciones que se le dan.
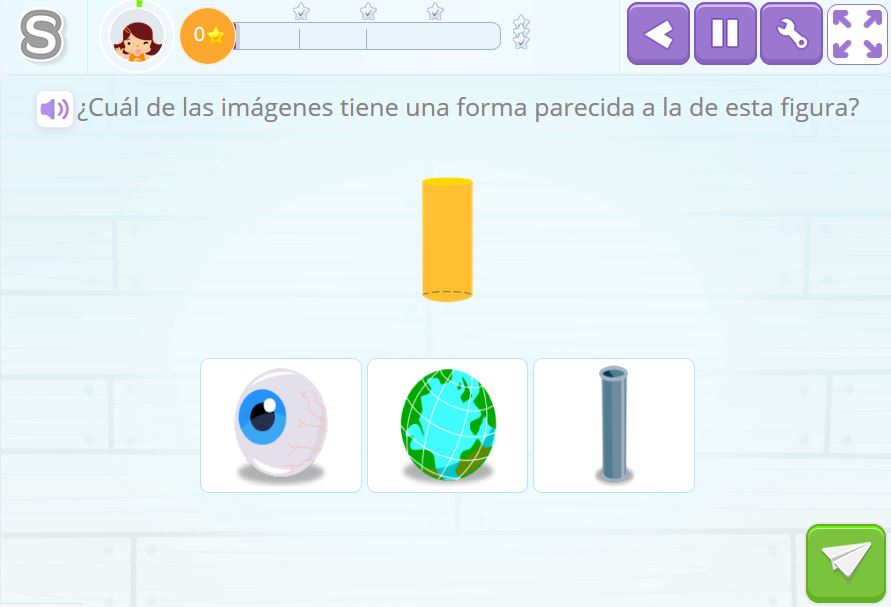
Comparar un cilindro con objetos reales
El alumno debe identificar que objeto del mundo real de los que se le presentan se asemeja a un cilindro. Como apoyo visual, se les presenta el cuerpo geométrico.
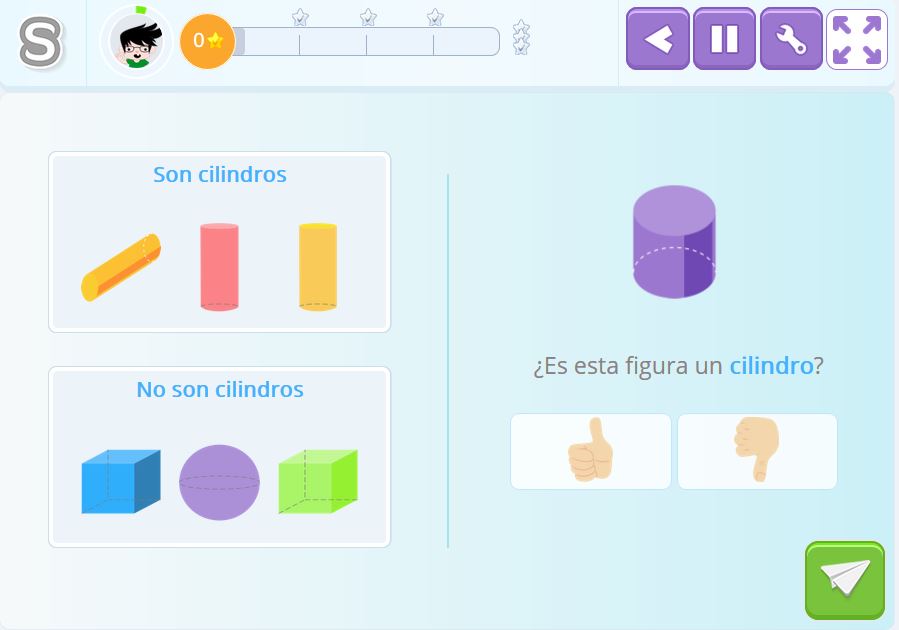
Identificar si un objeto real se parece o no a un cilindro
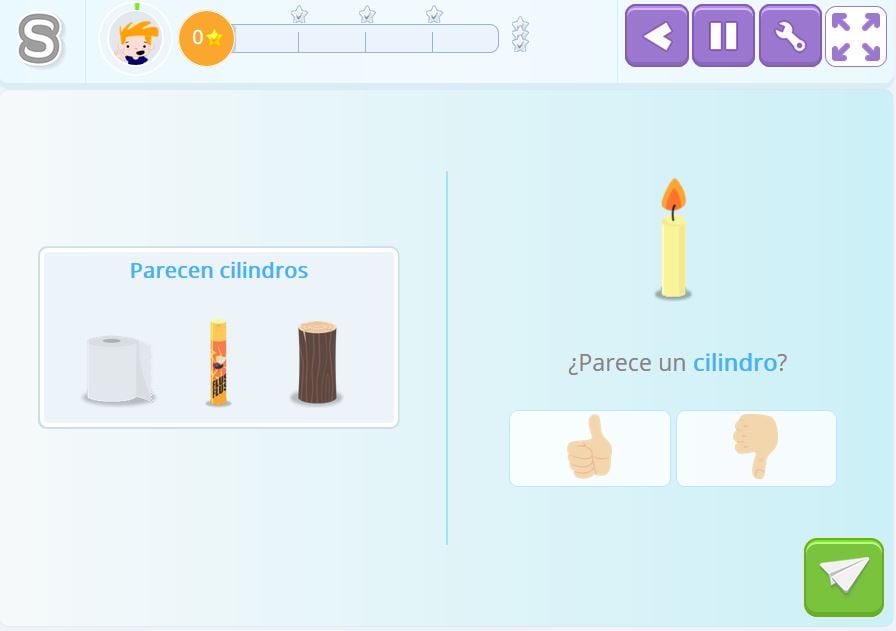
Identificar el nombre del cuerpo geométrico al que se parece un objeto real
Al alumno se le presenta un objeto de la vida cotidiana y se le indica que seleccione un nombre de entre todos los que se le dan.
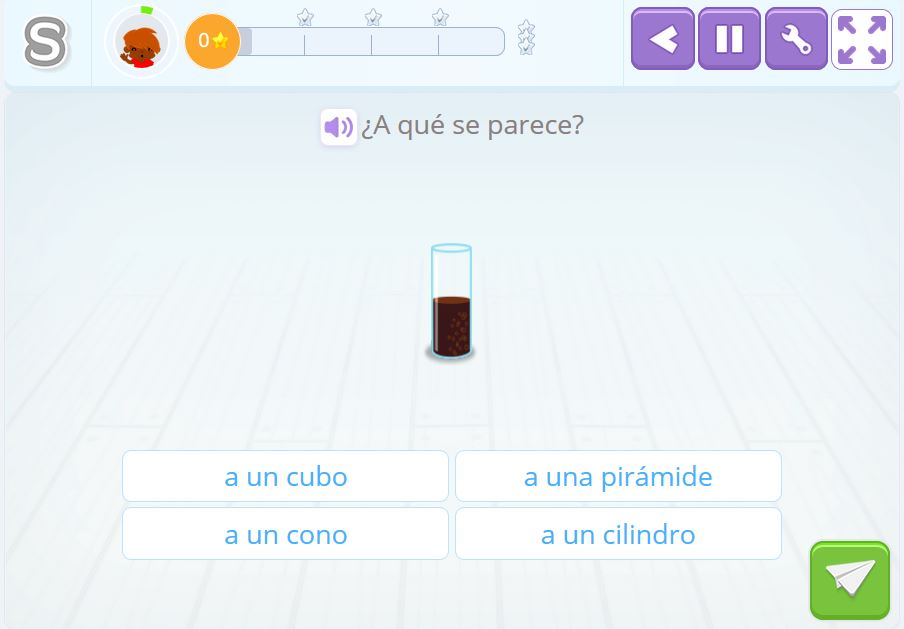
Estos son algunos ejemplos de las actividades de Smartick. Si quieres hacer más, regístrate en Smartick y prueba gratis nuestro método online para niños de 4 a 14 años.
Para seguir aprendiendo:
- El área de los cuerpos geométricos: aprende a calcularla
- Propiedad distributiva desde el punto de vista geométrico
- ¿Qué son las figuras geométricas sólidas o cuerpos geométricos?
- Propiedad conmutativa de la multiplicación y de la suma
- Geometría: Prismas








GRACIAS MAESTRO BUENA INFORMACIÒN 👍