Hoy vas a aprender qué es la simetría, veremos algunos ejercicios de simetría que hacen los alumnos de Smartick en sus sesiones y los errores típicos que se suelen cometer.
Índice
¿Qué es la simetría?
La simetría se refiere a una propiedad que describe la correspondencia exacta entre dos partes de un objeto, figura o función cuando se las compara a través de un punto, una línea o un plano. Es uno de los conceptos matemáticos que antes se empiezan a tratar en el colegio. Ya en educación infantil estudian y construyen figuras simétricas, sin utilizar una definición rigurosa.
Como veremos más adelante hay distintos tipos de simetrías. Vamos a empezar con la más conocida, la simetría respecto a una recta o simetría axial. Por eso, vamos a empezar dibujando una línea recta en un plano, que para el caso puede ser una hoja de cuadros como la de la siguiente imagen:
Decimos que una figura es simétrica respecto a una recta cuando cada punto a un lado de esa recta tiene otro punto al otro lado y a la misma distancia de esa recta.
Si queremos saber si una imagen presenta simetría respecto a una recta y la tenemos en una hoja de papel solo tenemos que doblarla por la recta. Si al doblar la hoja las figuras coinciden es que son simétricas respecto a esa recta. Si no coinciden, no lo son.
Si queremos construir una imagen simétrica en papel, empezamos por doblar el papel, y con un rotulador gordo, de los que la pintura traspasa el papel, pintamos la figura que queramos (no os olvidéis de proteger la mesa para que no llegue pintura). Luego desdoblamos el papel. La pintura ha traspasado también al otro lado y ha creado dos figuras simétricas respecto a la recta por la que doblamos el papel. Con el papel doblado coinciden exactamente. Alternativamente al rotulador, podemos utilizar unas tijeras.
Vídeo de figuras simétricas y ejes de simetría
Para entender mejor qué es simetría respecto a una recta os presentamos uno de nuestros tutoriales interactivos convertido en vídeo, por lo que deja de ser interactivo 🙁. Aún así tiene la gran ventaja de que se puede visualizar tantas veces como sea necesario y compartir. Si quieres acceder a los tutoriales interactivos de verdad, puedes hacerlo registrándote en Smartick, el método online de aprendizaje de matemáticas para niños de 4 a 14 años.
En el vídeo planteamos un verdadero taller de simetría. Lo puedes ver a continuación:
¿Qué es un eje de simetría?
Una figura simétrica puede tener uno o varios ejes de simetría, que sería la recta o rectas que parten la figura en dos partes simétricas.
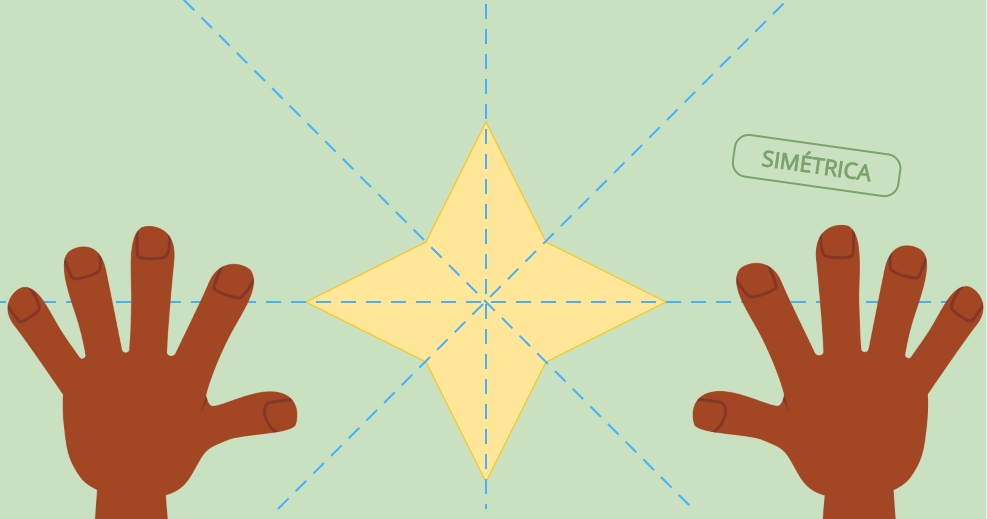
Tipos de simetría
Existen muchos tipos de simetría, pero nos vamos a fijar en estas tres que son las que se ven a lo largo de la etapa escolar:
- En primer lugar, la simetría axial o respecto a una recta es la que parte en dos los objetos o figuras a través de una línea recta, es decir, mediante un eje de simetría. Este tipo de simetría se podría asemejar a cuando nos miramos al espejo y reflejamos nuestra imagen en él.
- Decimos que una o varias figuras presentan simetría rotacional cuando no se alteran al girarlas un determinado ángulo. La estrella de cuatro puntas de la imagen anterior presenta simetría rotacional, porque si la giras 90º (o cualquier múltiplo de 90º) se ve igual.
- Un tercer tipo de simetría que se da en el plano es la simetría respecto a un punto o simetría central. Dos puntos son simétricos respecto de un punto -que llamaremos centro de simetría- si están a la misma distancia de éste y en la misma recta. La simetría central produce el mismo efecto que un giro de 180 grados.
Ejercicios de simetría en Smartick
En el post sobre nuevos contenidos de Smartick dábamos ejemplos de la secuencia de actividades de simetría. La dificultad varía con la forma de las figuras y la orientación del eje de simetría. Esta dificultad se va incrementando poco a poco, facilitando el aprendizaje y la comprensión de este concepto. Con estos ejercicios se favorece el desarrollo de la visión espacial y el razonamiento geométrico.
- Tenemos ejercicios donde hay que analizar si dos figuras son simétricas:
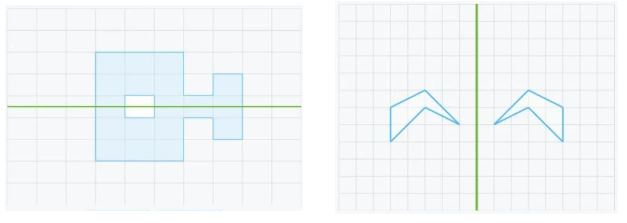
- En otros debemos construir figuras simétricas:
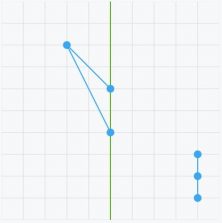
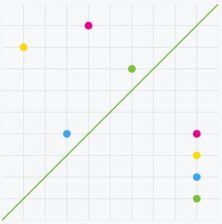
- O colocar una serie de puntos de manera simétrica respecto a un eje oblicuo:
Errores típicos
¿Son estas dos figuras simétricas respecto al eje? Hay dos errores que los alumnos suelen cometer al enfrentarse a esta pregunta.
- Pensar que si las figuras son idénticas entonces son simétricas:
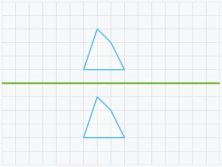
Para corregir este error (como decíamos más arriba) es útil pensar en la cuadrícula como un papel que se puede doblar por el eje de simetría. Si al doblarlo las figuras no coinciden es que no son simétricas. Otra manera es pensar que el eje es un espejo, como una figura no es el reflejo que proyectaría la otra sobre ese espejo, no son simétricas.
- Otra confusión común es pensar que si una figura es el reflejo especular de otra son simétricas independientemente de su posición respecto al eje de simetría:
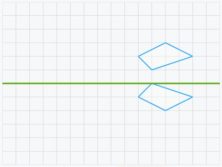
Podemos utilizar las mismas estrategias que antes para desechar este error. Si doblamos el papel por eje de simetría las figuras no coinciden. Y una figura no es el reflejo de la otra en el espejo del eje. Por tanto, estas dos figuras no son simétricas respecto al eje.
Simetría fuera de las matemáticas
La simetría nos rodea y está en todas partes:
- En un espejo o en el reflejo del agua. La imagen que se refleja es simétrica a la imagen real.
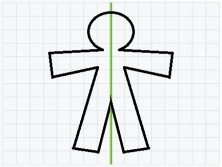
- En nosotros mismos: tenemos una mano derecha y una mano izquierda, una oreja derecha y otra izquierda, y cada pareja es simétrica. Nuestro cuerpo está dividido en dos partes simétricas, izquierda y derecha, respecto a un eje vertical que nos cruza por el centro desde la cabeza hasta los pies.
- La mayoría de las casas y edificios tienen fachadas simétricas respecto a un eje vertical.
- Los coches, las tostadoras, los teléfonos móviles, un vaso, un plato, una botella, la televisión, el sofá… La mayoría de objetos cotidianos tienen uno o más ejes de simetría.
- En el arte también encontramos simetría. Los autores la utilizan en pintura, escultura, música e infinidad de disciplinas.
- Incluso en la naturaleza. La mayoría de animales y plantas tienen algún tipo de simetría: bilateral, radial…
Si quieres aprender más geometría y matemáticas de primaria, adaptadas a tu nivel, entra en Smartick, regístrate y pruébalo gratis.
Para seguir aprendiendo:
- Identificación de figuras simétricas planas
- Trapezoide. Definición, tipos y ejercicios
- Figuras geométricas: el cuadrado
- Figuras geométricas: El círculo
- Figuras geométricas. Clasificación, tipos y ejemplos
Técnico Superior en Administración y Finanzas, Quiromasajista, Masajista Deportivo y Músico.
Forma parte del equipo de desarrollo de contenidos de Smartick.
Curioso por naturaleza, música y ciencia son dos de sus pasiones.
- Características de la práctica significativa - 23/03/2020
- Cómo representar fracciones en la recta numérica - 10/02/2020
- Diagramas de Venn en Smartick - 13/01/2020
MUY COMPLETO EL TEXTO Y EJEMPLOS, MUCHAS GRACIAS.
Me gusta la información
🆗🆗🆗🆗🆗🆗🆗🆗🆗
Gracias por la ayuda, me saqué diez
Es genial, pruébenlo
👍👍👍
Me gusta
Gracias por la información
Muy bien explicada la simetría.
Gracias, me sirvió mucho para mi trabajo de la escuela
Enhorabuena por la página, me parece muy acertada para explicar la simetría a los niños.