En esta entrada vamos explicar las propiedades de las potencias. Además, vamos a tratar de justificar la razón por la que se cumplen. Pero antes, recordemos qué es una potencia.
Índice
¿Qué es una potencia?
Una potencia es el producto de un número por sí mismo una cierta cantidad de veces. Dicho de otra forma, una potencia es una multiplicación de factores iguales. Esta idea se puede escribir de la siguiente forma: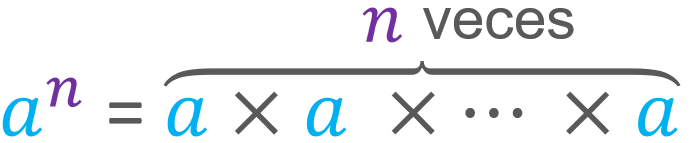
Al factor que se repite, a, se le conoce como base, mientras que a la cantidad de veces que se repite, n, se la llama exponente.
Puedes encontrar más información sobre qué son las potencias en este otro post. Una vez que hemos refrescado lo que es una potencia, sigamos con sus propiedades. Pero antes, vamos a establecer que la base tiene que ser distinta de 0… Después de todo, ¿a quién le interesa multiplicar por cero? 😀
Propiedades de las potencias
Producto de potencias de la misma base
A veces nos encontramos con productos de potencias que comparten la misma base. Por ejemplo:
23 × 25
62 × 67
En esos caso puede interesarnos recurrir a esta propiedad. Fíjate que la siguiente igualdad se cumple pues la multiplicación es asociativa y da igual el orden en el que se hagan los productos.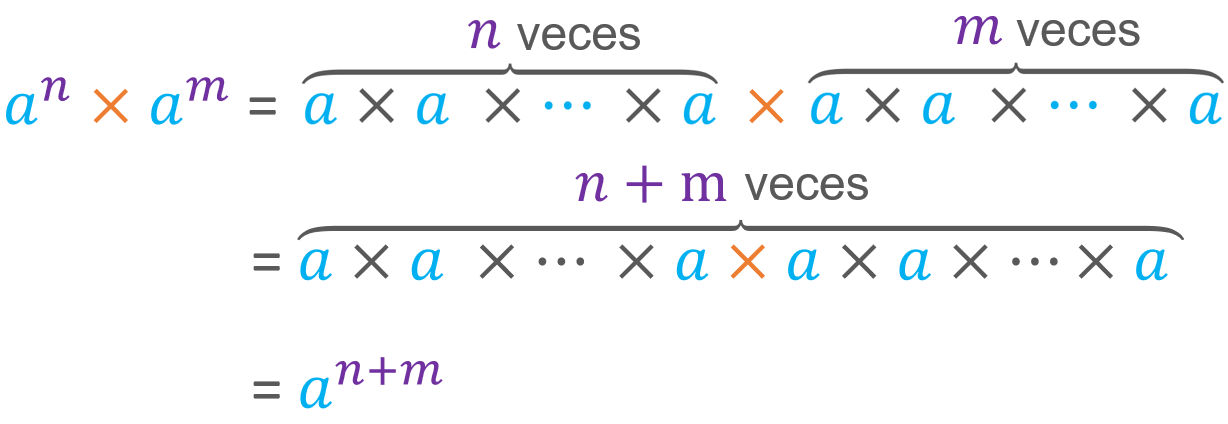
Esta propiedad puede leerse como «el producto de potencias de la misma base es igual a mantener la base y sumar los exponentes».
Fíjate en que también puede leerse de derecha a izquierda, es decir, que se pueden agrupar como se quieran los factores de una potencia para dar lugar al producto de otras dos con exponentes menores. Por ejemplo:
210 = 27 × 23
Cociente de potencias de la misma base
De forma similar a lo que ocurre con la multiplicación sucede también con la división. Recuerda que en una fracción se pueden simplificar los factores repetidos en el numerador y en denominador. ¡Fíjate!
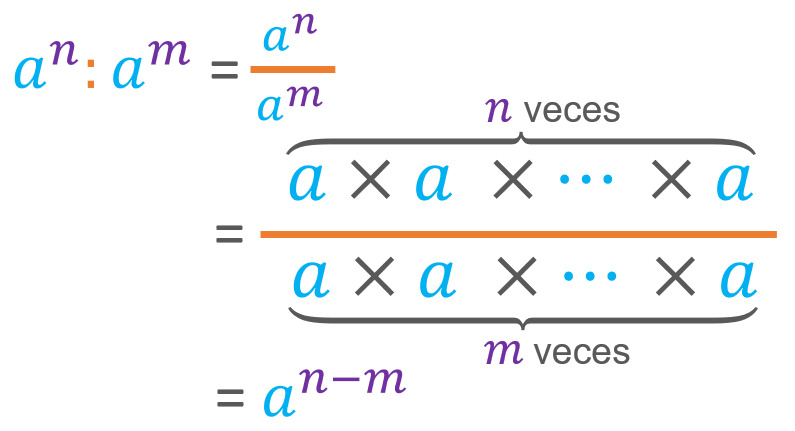
Esta propiedad se enuncia como «el cociente de potencias de la misma base es igual a mantener la base y restar los exponentes». Al igual que sucedía antes, esta igualdad se puede leer en el otro sentido y hacer, por ejemplo:
53 = 57 − 4 = 57 : 54
Potencias con exponente nulo
Muchos libros de texto, cuando explican las propiedades de las potencias, tratan esta situación como un caso aparte. En mi opinión no es necesario pues, si nos fijamos en la propiedad inmediatamente anterior, se puede entender una potencia con exponente nulo como un cociente de potencias iguales. Por ejemplo, 23 : 23. Pero también 52 : 52. Y 34657 : 34657
En general, cualquier base distinta de cero con cualquier exponente. ¿Y cuánto vale una fracción con el numerador y el denominador iguales? Pues 1, claro.
Por eso, se dice que «cualquier número elevado a 0 es 1».
Potencias de exponente negativo
De forma más o menos similar ocurre con las potencias de exponente negativo. Si nos fijamos en la propiedad del cociente de potencias de la misma base, si m es mayor que n, la resta n – m es un número negativo. Por eso, no es extraño que una potencia con exponente negativo sea una fracción con factores solo en el denominador.
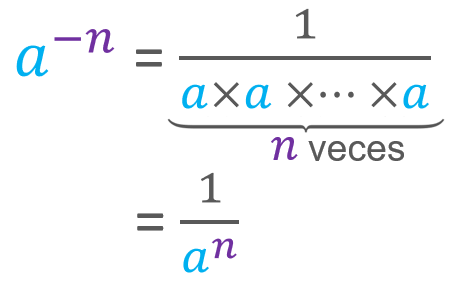
Es decir, que «una potencia con exponente negativo es igual a una fracción unitaria que tiene en el denominador la misma potencia pero con el exponente positivo».
Vídeo tutorial de potencias
En este video tutorial de Smartick sobre potencias puedes repasar y practicar con ejemplos. Si quieres resolverlo de manera interactiva, no dudes en registrarte en Smartick y probar nuestro método de manera gratuita.
Espero que esta entrada te haya ayudado a comprender las principales propiedades de las potencias. Si quieres seguir practicando cuestiones como esta y otras muchas más, adaptadas a tu nivel, únete ya mismo a la comunidad Smartick.
Para seguir aprendiendo:
- Propiedades de las potencias II
- Propiedades de las potencias I
- El signo en la potencia
- Potencias: qué son y para qué sirven con vídeo tutorial
- Potencias de base 10 y de base 100
Actualmente está cursando estudios de doctorado en Investigación en educación en la Universidad de Valladolid.
Es profesor de didáctica de la matemática en la Universidad de Valladolid y forma parte del equipo de desarrollo de contenidos de Smartick.
Entre sus aficiones destacan el tenis, el jazz y la escritura.
- Propiedades de las potencias - 13/04/2020
- El porqué de los criterios de divisibilidad - 02/03/2020
- Por qué son importantes los ejemplos en la enseñanza de las matemáticas - 27/01/2020