Números primos: cómo encontrarlos con la criba de Eratóstenes

En el post de hoy vamos a aprender a encontrar números primos con el método de la criba de Eratóstenes.

¿Qué es un número primo?

Un número primo es aquel que sólo es divisible por 1 y por sí mismo. Algo tan sencillo como eso. Lo complicado es que no existe una fórmula matemática que asegure si lo es o no.

Pensemos en un número elevado como 191.587, ¡no tenemos una fórmula que determine si este número es primo!

Tendríamos que ir comprobando si tiene algún divisor y por lo tanto es compuesto. En ese caso, lo descartaríamos como número primo.

Para los primeros números primos (2, 3, 5, 7, 11), sería asequible comprobar si tienen divisores con ayuda los criterios de divisibilidad, pero para números más altos ya no sería tan fácil.

¡Imagínate tener que comprobar todos los divisores de un número tan alto! ¡Sería una locura!

Criba de Eratóstenes

El matemático griego Eratóstenes ( siglo III a.C.) ideó una manera rápida de obtener todos los números primos hasta uno concreto. Se trata de un procedimiento denominado Criba de Eratóstenes, que veremos cómo funciona encontrando todos los números primos entre 1 y 100.

Teniendo todos los números en una tabla, se trata de ir buscando los que sean múltiplos de algún número y por tanto sean compuestos, para descartarlos como primos. Los números que nos queden sin descartar, serán declarados números primos.

La criba de Eratóstenes se para en el momento en que el cuadrado del número a investigar es mayor que el último número de la lista (en nuestro caso el 100).

Como 11²  = 121 y 121>100, cuando lleguemos al número 11, podremos parar de buscar.

Números primos entre 1 y 100 con la Criba de Eratóstenes

Empezamos colocando los números del 1 al 100 en una tabla como esta, donde resulta muy fácil observar los patrones que forman los múltiplos de cada número. Marcamos el 1, que no se considera un número primo.

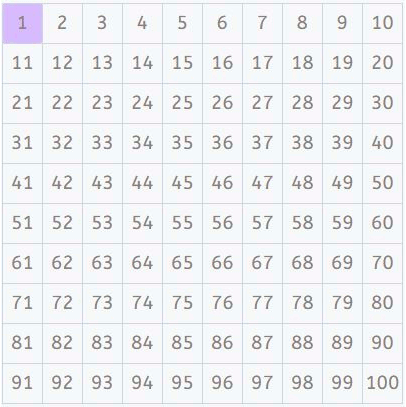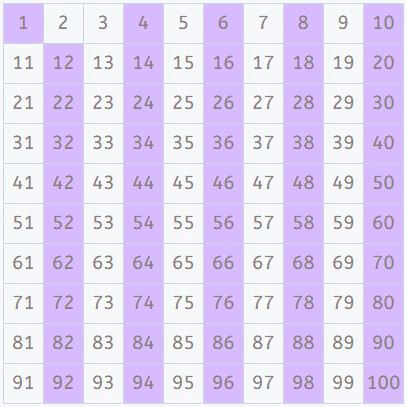
Múltiplos de 2

Primero, buscamos los múltiplos de 2 y los marcamos (exceptuando el 2, que sabemos que sólo tiene como divisores 1 y 2, así que es primo). Todos estos números serán compuestos. ¿Has visto qué patrón tan bonito tienen los números pares?

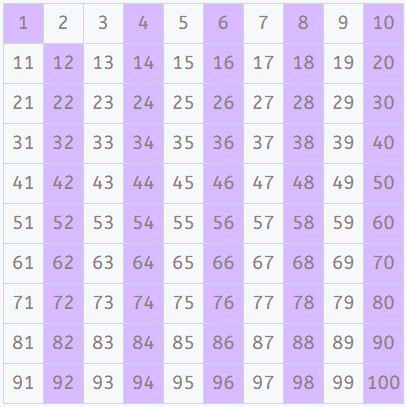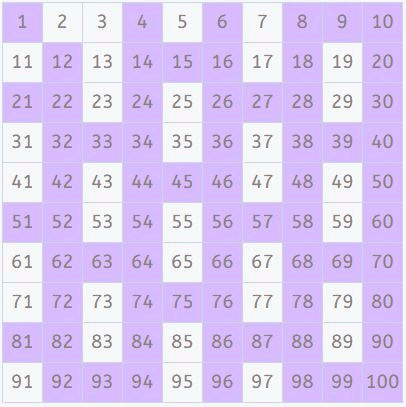
Múltiplos de 3

Ahora, de los que quedan, buscamos los múltiplos de 3 y los marcamos (exceptuando el 3, que es primo). Una manera fácil es ir contando de 3 en 3. También aquí observamos un patrón interesante.

Múltiplos de 5

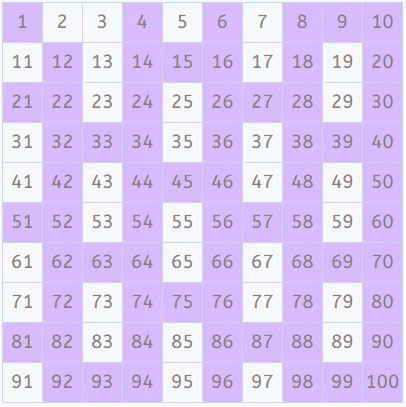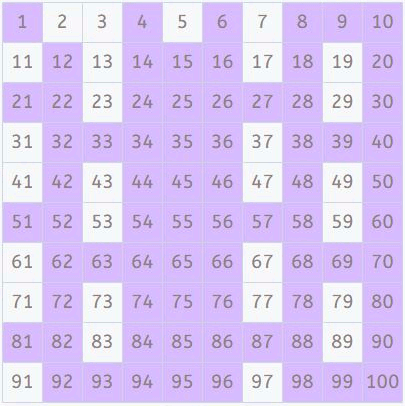
Ahora es el turno de buscar los múltiplos de 5 (de 4 no haría falta, porque todos los múltiplos de 4 también son múltiplos de 2, así que ya los hemos marcado anteriormente). Es fácil encontrarlos, ya que son todos los acabados en 0 o 5. Dejamos el 5 sin marcar, ya que es primo.

Múltiplos de 7

Vamos ahora con los múltiplos de 7 (los de 6 no hace falta buscarlos, ya que 6 = 2 x 3 y ya hemos buscado los de 2 y 3). Dejamos el 7 sin marcar, ya que es primo.

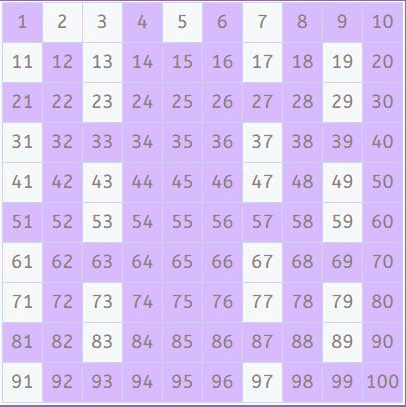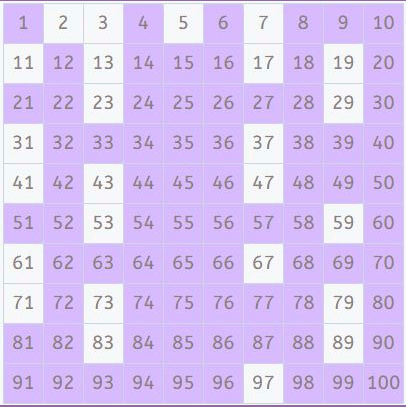
Como ya solo nos queda buscar los múltiplos de 8, 9 y 10 y éstos son compuestos y múltiplos de números que ya hemos buscado, llegamos al número 11, donde dijimos al principio que debíamos parar. Así que ¡ya hemos terminado!

Lista de números primos entre 1 y 100

Podemos determinar entonces que los números que nos han quedado sin marcar, son todos números primos. Así que ya tenemos la lista de números primos entre 1 y 100:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 y 97.

¿Has visto qué fácil resulta buscar números primos con este método? Eso sí, solo para números pequeños, si no puede resultar muy tedioso. Pero imagina lo fácil que será para una computadora.

Mira lo divertido que cuentan el procedimiento en el libro «El diablo de los números«. Una lectura muy recomendable si quieres aprender muchas matemáticas de una manera muy entretenida.

Por último, aquí tienes una imagen con los pasos del ejemplo que hemos visto, para que los tengas todos juntos.

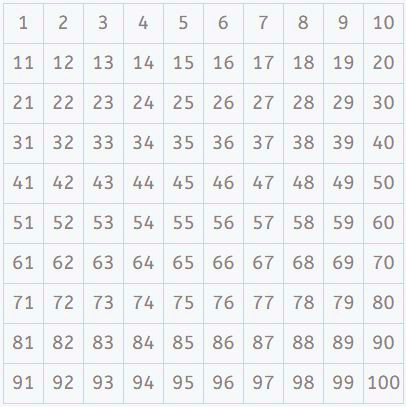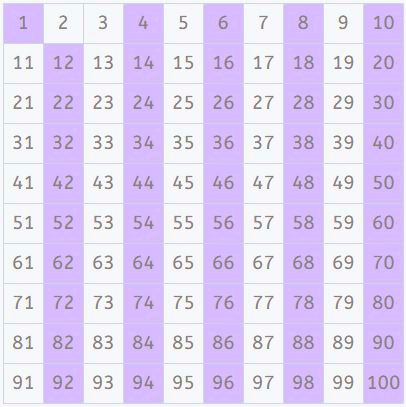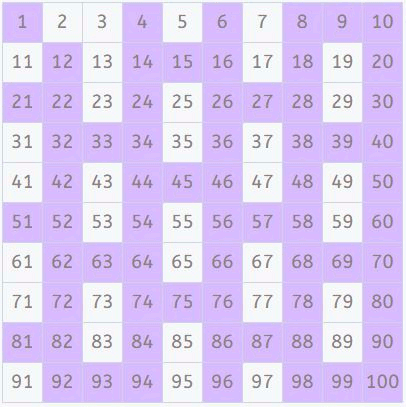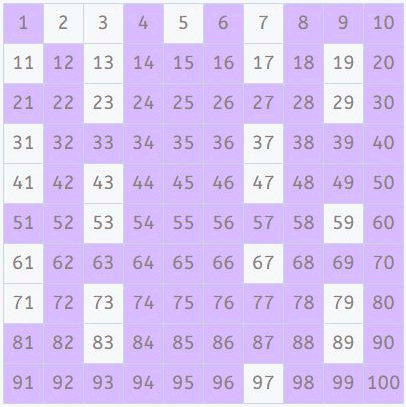
¿Qué te ha parecido este post? ¿Conocías la Criba de Eratóstenes? Te animo a que la pruebes tú mismo descargando e imprimiendo esta tabla de números del 1 al 100. Puedes ir tachando los números que vayas descartando como primos.

Si quieres seguir aprendiendo y practicando más matemáticas de primaria, entra en Smartick, regístrate y prueba gratis nuestro método de aprendizaje online que se adapta a cada alumno.

Para seguir aprendiendo:

• Números primos y números compuestos
• Factorizar en números primos
• Números primos: actividades en Smartick
• Números primos y números compuestos. Qué son y ejemplos
• Curiosidades sobre los números primos

La diversión es la forma favorita de aprender de nuestro cerebro

Diane Ackerman

Smartick ayuda a tus hijos a aprender de manera divertida

• 15 minutos diarios
• Se adapta al nivel de cada niño
• Millones de estudiantes desde 2009

Prueba GRATIS 7 días

• Acerca de
• Últimas entradas

Marisa Reguero

Licenciada en Matemáticas y monitora de ocio y tiempo libre, por lo que cree en el aprendizaje a través del juego y la experimentación y le apasiona hacer de las matemáticas una asignatura amigable para los niños.
Forma parte del equipo de desarrollo de contenidos de Smartick Matemáticas.
Amante de la naturaleza, el yoga y el baile.

Últimas entradas de Marisa Reguero (ver todo)

• Valor absoluto de un número - 28/10/2019
• Cálculo de áreas de polígonos - 16/09/2019
• Potencias y su representación con regletas - 08/07/2019