Máximo común divisor (MCD): qué es, características y cómo calcularlo

¿Preparado para aprender qué es y cómo se calcula el máximo común divisor? En este post te lo explicamos. Con los ejemplos y vídeos que te presentamos entenderás mucho mejor el MCD. ¡Vamos!

Qué es el máximo común divisor (MCD)

En matemáticas, se denomina máximo común divisor o MCD al mayor número que divide exactamente a dos o más números a la vez. Como hablamos del mayor número solo tendremos en cuenta los divisores positivos.

También podemos decir que el máximo común divisor de dos números «A» y «B», es el número mayor que los divide a los dos, tanto al número A como al número B.

Por ejemplo diremos que el máximo común divisor de 18 y 24 es 6, porque 6 es el mayor de los divisores comunes de 18 y 24 y lo escribimos MCD (18,24) = 6

Se tienen en cuenta los números en los que las divisiones den de resto cero. Puedes repasar las divisiones por una cifra si lo prefieres para ayudarte a recordar las partes que componen una división.

Vídeo sobre el máximo común divisor

Para entender mejor qué es el MCD de dos números te invito a que veas el siguiente vídeo. Es uno de nuestros tutoriales interactivos convertido en vídeo, por lo que deja de ser interactivo 🙁.

Aún así tiene la gran ventaja de que se puede visualizar tantas veces como sea necesario y compartir. Si quieres acceder a los tutoriales interactivos de verdad, puedes hacerlo registrándote en Smartick, el método online de aprendizaje de matemáticas para niños de 4 a 14 años.

Para qué se usa el máximo común divisor

MCD para simplificar fracciones

Una de las utilidades que tiene el máximo común divisor es simplificar fracciones.

Por ejemplo, para simplificar la fracción 12/18, se calcula primero el Máximo Común Divisor de 12 y 18 que es 6.

Después tenemos que dividir el numerador y el denominador de la fracción inicial entre 6 para obtener la fracción simplificada que es 2/3.

MCD para calcular el mínimo común múltiplo (mcm)

El máximo común divisor también se puede utilizar para calcular el mínimo común múltiplo de dos números, su mcm.

Esto es porque el producto del máximo común divisor de dos números por el mínimo común múltiplo (de los mismos números) es igual al producto de esos dos números.

Veámoslo con un ejemplo. Como hemos dicho antes MCD (12,18) = 6 como 12 × 18 = 216, su mínimo común múltiplo tiene que ser 36 porque 6 × 36 = 216.

MCD para resolver problemas

Sin duda, para lo que más vas a utilizar el MCD es para resolver problemas.

Términos

Ahora, vamos a explicar algunos de los conceptos que se emplean para calcular el MCD de varios números, es importante aprenderlos para que nos sean familiares y sepamos en cada momento de lo que estamos hablando.

Divisor

El divisor de un número es el valor que divide al número en partes exactas, es decir, que el resto sea cero.

Vamos a ver un ejemplo de esto:

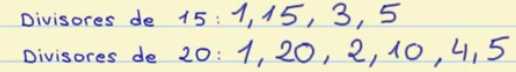
Primero, calculamos los divisores de 15:

• 15 / 1 = 15, por lo que 1 y 15 son divisores de 15.
• 15 / 2 = 7, el resto es 1, por lo que 2 no es divisor de 15.
• 15 / 3 = 5, por lo que 3 y 5 son divisores de 15.
• 15 / 4 = 3, el resto es 3, por lo que 4 no es divisor de 15.

Ahora deberíamos dividir entre 5 pero como ya lo tenemos como divisor, ya hemos acabado de calcular los divisores de 15.

Por tanto, los divisores de 15 son: 1, 3, 5 y 15.

También vamos a calcular los divisores de 20:

• 20 / 1 = 20, por lo que 1 y 20 son divisores de 20.
• 20 / 2 = 10, por lo que 2 y 10 son divisores de 20.
• 20 / 3 = 6, el resto es 2, por lo que 3 no es un divisor de 20.
• 20 / 4 = 5, por lo que 4 y 5 son divisores de 20.

Ahora deberíamos dividir entre 5 pero como ya lo tenemos como divisor, ya hemos acabado de calcular los divisores de 20.

Es decir, los divisores de 20 son: 1, 2, 4, 5, 10 y 20.

Divisor común

Es un número que es divisor a la vez de dos o más números, es decir, es un divisor común a esos números.

Si seguimos con el ejemplo anterior, en el que hemos calculado los divisores de 15 y de 20, ahora vamos a ver cuales son los divisores comunes.

Divisores de 15: 1, 3, 5 y 15.

Divisores de 20: 1, 2, 4, 5, 10 y 20.

¿Qué divisores tienen en común 15 y 20?

En este caso, si te fijas, los divisores comunes que tienen 15 y 20 son el 1 y el 5.

Máximo común divisor

Como hemos visto al inicio del post, el máximo común divisor es el número mayor entre los divisores comunes.

Vamos a ver cuál es el máximo común divisor del ejemplo anterior, el MCD (15,20).

Divisores de 15: 1, 3, 5 y 15.

Divisores de 20: 1, 2, 4, 5, 10 y 20.

Ya sabes que los divisores comunes de 15 y 20 son el 1 y el 5, ahora de entre esos dos números (1 y 5) tienes que elegir el número mayor, que es el 5. Por lo que, el máximo común divisor de 15 y 20 es 5.

Cómo hacer el máximo común divisor

Para saber cuál es el máximo común divisor de dos o más números existen varios métodos, vamos a ver dos.

Método 1 para calcular el MCD

Es el que venimos utilizando en los ejemplos de más arriba. Para ello es importante fijarnos muy bien lo que significa máximo común divisor.

• Escribimos todos los divisores de cada número, y de éstos señalamos los divisores comunes.
• El divisor mayor será el MCD de esos números.

El inconveniente de este método es que un número grande puede tener muchos divisores y escribirlos todos puede ser muy pesado. La ventaja que tiene es que si lo tienes en cuenta, a veces no tendrás que calcular nada, fíjate, si te piden el máximo común divisor de tres números y resulta que uno divide a los demás, ya tienes el máximo común divisor. Por ejemplo el máximo común divisor de 36, 12, y 84. Como 12 divide a los tres, no podrá haber ningún divisor común mayor.

Método 2 para calcular el MCD

Descomposición de factores o descomposición en números primos.

• Descomponemos cada número en factores primos.
• Después, señalamos los factores comunes.
• A continuación, en cada uno de los comunes, escogemos el factor con menor exponente.
• Y por ultimo, multiplicamos los factores elegidos.

Vamos a ver un ejemplo:

Calculamos el M.C.D de 8 y 12.

Como ves, hemos señalado los factores comunes, en este caso es el 2, pero debes tener cuidado, tienes que fijarte siempre en el de menor exponente (2²), que es igual a 4. Además, si quieres puedes recordar cómo se hace la descomposición factorial y las potencias.

Vídeo para aprender a calcular el MCD a través de la descomposición en factores

En el siguiente vídeo puedes ver cómo Eva y Leo ayudan a las familias de su colegio que necesitan material escolar y libros utilizando el máximo común divisor.

Es uno de los tutoriales interactivos de Smartick convertido en vídeo. Si quieres acceder al tutorial interactivo y resolverlo tú mismo, puedes hacerlo registrándote en Smartick, el método online de aprendizaje de matemáticas adaptado a tu nivel y ritmo.

Ejemplos y ejercicios

Vamos a ver varios ejemplos de los ejercicios en los que utilizaremos los dos métodos que hemos explicado antes. El método 1 buscando los divisores de un número y el método 2 realizando la descomposición en factores para poder calcular el máximo común divisor.

Calcular el MCD de 6 y 9 con el método 1.

1. Escribimos todos los divisores de cada número (de 6 y de 9), anteriormente ya hemos explicado como se sacan los divisores de un número.
2. Señalar todos los divisores comunes.
3. Elegir el divisor común mayor.

Por lo tanto, el MCD de 6 y 9 = 3 

Calcular el MCD de 16 y 21 con el método 2.

1. Factorizamos los números (16 y 21).
2. Escribimos en factores cada uno de los números, el 16 y el 21.
3. Ver cuáles son los factores comunes. En este caso, como ves, los números 16 y 21 no tienen factores comunes. Cuando no hay factores comunes entre los números el máximo común divisor es 1.

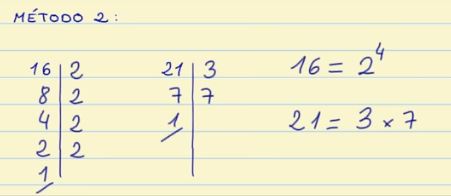
MCD de 16 y 21 = 1

Calcular el MCD de 14, 36 y 12 con el método 2.

1. Descomponemos los números en factores primos.
2. Escribimos en factores cada uno de los números (14, 36 y 12).
3. Elegir los factores comunes entres los tres números. En esta caso, el único factor común entre 14, 36 y 12 es el 2.
4. Coger entre los factores comunes el que tiene menor exponente. El de menor exponente es el 2.

Por lo tanto, el Máximo Común Divisor entre 14, 36 y 12 = 2.

¡Anímate a practicar de forma divertida!

Y si quieres aprender muchas más matemáticas de primaria, adaptadas a tu nivel, entra en Smartick y pruébalo gratis.

Para seguir aprendiendo:

• MCD o Máximo Común Divisor
• Para qué sirve la descomposición factorial
• ¿Qué es la descomposición factorial?
• ¿Qué es el mínimo común múltiplo (mcm)?
• Números primos y números compuestos

La diversión es la forma favorita de aprender de nuestro cerebro

Diane Ackerman

Smartick ayuda a tus hijos a aprender de manera divertida

• 15 minutos diarios
• Se adapta al nivel de cada niño
• Millones de estudiantes desde 2009

Prueba GRATIS 7 días

• Acerca de
• Últimas entradas

Sara Sánchez Ruesgas

Licenciada en Físicas por la Universidad Autónoma de Madrid.
Sara es parte del equipo de desarrollo de contenidos y didáctica de Smartick Matemáticas, responsable de las áreas de álgebra y lógica.

Últimas entradas de Sara Sánchez Ruesgas (ver todo)

• Tablas de multiplicar: cómo construirlas con una cuadrícula - 28/08/2017
• Problemas de matemáticas en Smartick de quinto de primaria - 31/07/2017
• Símbolos matemáticos para representar operaciones y relaciones entre valores - 03/07/2017